МЕТОДИКИ ФОРМИРОВАНИЯ ПОРТФЕЛЯ
Каждый инвестор формирует портфель исходя из поставленных им целей, а также согласно определенным параметрам доходности и уровня риска. Решение инвестора включить в состав портфеля ту или иную ценную бумагу принимается в условиях неопределенности, доходность финансового инструмента и рынка в среднем показатель динамичный, что затрудняет возможность прогнозирования будущей доходности отдельной ценной бумаги и портфеля в целом. Тем не менее, при помощи разработанных различными учеными методик инвестор может с наибольшей степенью вероятности рассчитать какой в будущем будет доходность портфеля и определить его уровень риска. Наиболее известны и применимы методики Марковица, Блека и У.Шарпа. Модель Марковица. Оптимальный портфель - эффективный портфель, которому инвестор отдает предпочтение, поскольку параметры риска/вознаграждения этого портфеля приближены к функции полезности инвестора.[5] Цель оптимального портфеля обеспечить оптимальное сочетание выгодности, надежности и ликвидности ценных бумаг, финансовых вложений для инвестора. На практике используют множество методик формирования оптимальной структуры портфеля ценных бумаг. Большинство из них основано на методике Марковица. Он впервые предложил математическую формализацию задачи нахождения оптимальной структуры портфеля ценных бумаг в 1951 году, за что позднее был удостоен Нобелевской премии по экономике. Основными постулатами, на которых построена классическая портфельная теория, являются следующие: · рынок состоит из конечного числа активов, доходности которых для заданного периода считаются случайными величинами; · инвестор в состоянии, например, исходя из статистических данных, получить оценку ожидаемых (средних) значений доходностей и их попарных ковариаций и степеней возможности диверсификации риска; · инвестор может формировать любые допустимые (для данной модели) портфели. Доходности портфелей являются также случайными величинами; · сравнение выбираемых портфелей основывается только на двух критериях - средней доходности и риске; · инвестор не склонен к риску в том смысле, что из двух портфелей с одинаковой доходностью он обязательно предпочтет портфель с меньшим риском. Основная идея модели Марковица заключается в том, чтобы статистически рассматривать будущий доход, приносимый финансовым инструментом, как случайную переменную, то есть доходы по отдельным инвестиционным объектам случайно изменяются в некоторых пределах. Тогда, если неким образом случайно определить по каждому инвестиционному объекту вполне определенные вероятности наступления, можно получить распределение вероятностей получения дохода по каждой альтернативе вложения средств. Это получило название вероятностной модели рынка. Для упрощения модель Марковица полагает, что доходы распределены нормально. По модели Марковица определяются показатели, характеризующие объем инвестиций и риск, что позволяет сравнивать между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций.[6] В качестве ожидаемого дохода из ряда возможных доходов на практике используют наиболее вероятное значение, которое в случае нормально распределения совпадает с математическим ожиданием. Математическое ожидание дохода по i -й ценной бумаге (mi) рассчитывается следующим образом:
где Ri – возможный доход по i -й ценной бумаге, руб.; Pij - вероятность получения дохода; n – количество ценных бумаг.
Для измерения риска служат показатели рассеивания, поэтому, чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен. Мерой рассеивания является среднеквадратическое отклонение:
В отличие от вероятностной модели, параметрическая модель допускает эффективную статистическую оценку. Параметры этой модели можно оценить исходя из имеющихся статистических данных за прошлые периоды. Эти статистические данные представляют собой ряды доходностей за последовательные периоды в прошлом. Любой портфель ценных бумаг характеризуется двумя величинами: ожидаемой доходностью
mi - ожидаемая доходность i -й ценной бумаги, %; тр — ожидаемая доходность портфеля, %. и мерой риска - среднеквадратическим отклонением доходности от ожидаемого значения
где σр - мера риска портфеля; σ ij - ковариация между доходностями i -й и j -й ценных бумаг; Xi и Xj - доли общего вложения, приходящиеся на i -ю и j -ю ценные бумаги; п - число ценных бумаг портфеля. Ковариация доходностей ценных бумаг (σ ij) равна корреляции между ними, умноженной на произведение их стандартных отклонений:
где pij - коэффициент корреляции доходностей i -ой и j -ой ценными бумагами; σ j иσ i - стандартные отклонения доходностей i -ой и j -ой ценных бумаг. Для i = j ковариация равна дисперсии акции. Рассматривая теоретически предельный случай, при котором в портфель можно включать бесконечное количество ценных бумаг, дисперсия (мера риска портфеля) асимптотически будет приближаться к среднему значению ковариации. Графическое представление этого факта представлено на рис. 1.
Рис. 1. Риск портфеля и диверсификация
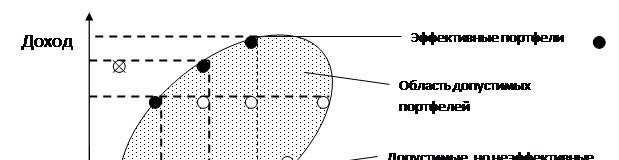
Совокупный риск портфеля можно разложить на две составные части: рыночный риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени, и собственный риск, который можно избежать при помощи диверсификации. При этом сумма вложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений, т.е. сумма относительных долей в общем объеме должна равняться единице. Проблема заключается в численном определении относительных долей акций и облигаций в портфеле, которые наиболее выгодны для владельца. Марковиц ограничивает решение модели тем, что из всего множества «допустимых» портфелей, т.е. удовлетворяющих ограничениям, необходимо выделить те, которые рискованнее, чем другие. При помощи разработанного Марковицем метода критических линий можно выделить неперспективные портфели. Тем самым остаются только эффективные портфели. Отобранные таким образом портфели объединяют в список, содержащий информацию о структуре портфеля, а также о доходе и риске портфелей. Объяснение того факта, что инвестор должен рассмотреть только подмножество возможных портфелей, содержится в следующей теореме об эффективном множестве: «Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает максимальную ожидаемую доходность для некоторого уровня риска и минимальный риск для некоторого значения ожидаемой доходности». Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством. На рис. 2 представлены недопустимые, допустимые и эффективные портфели, а также линия эффективного множества.
Рис. 2. Допустимое и эффективное множество портфелей
В модели Марковица допустимыми являются только стандартные портфели (без коротких позиций). Используя более техническую терминологию, можно сказать, что инвестор по каждому активу находится в длинной позиции. Длинная позиция - это обычно покупка актива с намерением его последующей продажи (закрытие позиции). Такая покупка обычно осуществляется при ожидании повышения цены актива в надежде получить доход от разности цен покупки и продажи. Из-за недопустимости коротких позиций в модели Марковица на доли ценных бумаг в портфели накладывается условие неотрицательности. Поэтому особенностью этой модели является ограниченность доходности допустимых портфелей, т.к. доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен. Для выбора наиболее приемлемого для инвестора портфеля ценных бумаг можно использовать кривые безразличия. В данном случае эти кривые отражают предпочтение инвестора в графической форме. Предположения, сделанные относительно предпочтений, гарантируют, что инвесторы могут указать на предпочтение, отдаваемое одной из альтернатив или на отсутствие различий между ними. Если же рассматривать отношение инвестора к риску и доходности в графической форме, откладывая по горизонтальной оси риск, мерой которого является среднеквадратическое отклонение (σр), а по вертикальной оси - вознаграждение, мерой которого является ожидаемая доходность (rр), то можно получить семейство кривых безразличия. Располагая информацией об ожидаемой доходности и стандартных отклонениях возможных портфелей ценных бумаг, можно построить карту кривых безразличия, отражающих предпочтения инвесторов. Карта кривых безразличия - это способ описания предпочтений инвестора к возможному риску полностью или частично потерять вкладываемые в портфель ценных бумаг деньги или получить максимальны доход. Определение кривой безразличия клиента является нелегкой задачей. На практике ее часто получают в косвенной или приближенной форме путем оценки уровня толерантности риска, определяемой как наибольший риск, который инвестор готов принять для данного увеличения ожидаемой доходности. Поэтому, с точки зрения методологии модель Марковица можно определить как практически-нормативную, что не означает навязывания инвестору определенного стиля поведения на рынке ценных бумаг. Задача модели заключается в том, чтобы показать, как поставленные цели достижимы на практике.[7]
|

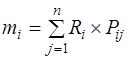 , (6.1)
, (6.1)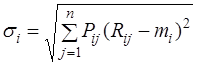 , (6.2)
, (6.2) , (6.3)
, (6.3) где Xi - доля общего вложения, приходящаяся на i -ю ценную бумагу;
где Xi - доля общего вложения, приходящаяся на i -ю ценную бумагу;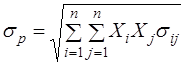 , (6.4)
, (6.4) , (6.5)
, (6.5)