PROGRAM PRG7_8;

CONST N = 100;

VAR А, В: ARRAY[1..N, 1..N] OF INTEGER;

К, М, I, J: INTEGER;

BEGIN

WRITE('BBEДИTE РАЗМЕР МАТРИЦЫ М = ');

READLN (M);

WRITELN('ИСХОДНАЯ МАТРИЦА');

К:= 1;

FOR I:= 1 ТО М DO

FOR J:= 1 TO M DO

BEGIN

A[l, J]:= K;

К:= K+1;

IF J<M THEN WRITE(A[I, J]: 4)

ELSE WRITELN(A[I, J]: 4)

END;

WRITELN('MATPИЦA ПОСЛЕ ПОВОРОТА НА 180 ГРАДУСОВ');

FOR I:= 1 ТО М DO

FOR J:= 1 TO M DO

BEGIN

B[l, J]:= A[M+1-I, M+1-J];

IF J<M THEN WRITE(B[I, J]: 4)

ELSE WRITELN(B[I, J]: 4)

END;

END.

Для решения задачи:

- формируем тело программы и описываем переменные;

- вводим размеры массива А и присваиваем значения его эле­ментам;

- присваиваем значения элементам матрицы В и выводим их на экран.

Переменные:

А, В - двумерные массивы;

М - количество строк и столбцов массива;

I, J - переменные цикла;

К - вспомогательная переменная.

 

ВВЕДИТЕ PA3MEР МАТРИЦЫ М = 4

ИСХОДНАЯ МАТРИЦА

1 2 3 4

5 6 7 8

9 10 11 12

13 14 15 16

МАТРИЦА ПОСЛЕ ПОВОРОТА НА 180 ГРАДУСОВ

16 15 14 13

12 11 10 9

8 7 6 5

4 3 2 1

 

Рис. 7.6. Результат работы PRG7_8

Задача 7.9 Дана квадратная матрица N x N, состоящая из натуральных чисел. Зеркально отразить ее эле­менты относительно горизонтальной оси симмет­рии. Вывести результат на экран.

Рассмотрим вначале матрицу 3 х 3 и посмотрим, что происхо­дит с элементами при зеркальном отражении.

А 11	А 12	А 13	Þ	А 31	А 32	А 33
А 21	А 22	А 23	А 21	А 22	А 23
А 31	А 32	А 33	А 11	А 12	А 13

Если считать, что после преобразования у нас появилась новая матрица В, то соответствие между элементами устанавливается следующим образом:

В 11 «А 31

В 12 «А 32

В 21 «А 21

В 22 «А 22 и т. д., т. е. В [I, J] «A [L, М].

Внимательно изучив соответствие, можно утверждать, что для элементов матрицы N х N справедлива следующая система урав­нений: 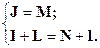Отсюда правило преобразования элементов выглядит следу­ющим образом: В [ I, J ] = А [ N+1–I, J ].

Программа, решающая данную задачу, так: