Малювання за допомогою кривих

Графічний елемент для створення кривих має дві графічні функцій: quadraticCurveTo (х, у) і bezierCurveTo (cp1x, cp1y, cp2x, cp2y, х, у). Обидві функції використовують контрольні точки для визначення кривої шляху при розробці від однієї точки до іншої.

1. У папці HTML5_05lessons, відкрийте 05_drawingcurves.HTML-файл і збережіть копію файлу 05_drawingcurves_work.html. Код збігається з кодом попереднього прикладу: для створення графічного елементу і збереження 2D змінної для повторного використання. У цій вправі ви будете використовувати декілька форм для створення квіткової композиції.

2. У разі об’яви, додайте наступний код, щоб намалювати прямокутник, який описує полотно.

ctx.strokeRect (0, 0, 300, 300);

3. Додайте наступні рядки після рядка з попереднього кроку і зробіть стебло квітки:

ctx.fillStyle = "RGB (0173104);

ctx.moveTo (145, 150);

ctx.quadraticCurveTo (120, 200, 170, 280);

ctx.lineTo (190, 280);

ctx.quadraticCurveTo (125, 190, 155, 150);

ctx.fill ();

Перший рядок коду змінює заливки на зелений. Решта рядків коду визначають відправні точки, криві і лінії стовбурових форм.

4. Виберіть File> Save. Включіть ваш браузер, а потім перегляньте HTML-сторінку. Ви побачите як і на наступному малюнку:

Рисунок 10 – Зелена форма стебла квітки

Тепер ви створите пелюстку за допомогою функції bezierCurveTo, яка використовує дві контрольні точки, на відміну від однієї контрольної точки, що використовується з функцією quadraticCurveTo. Крім того, ви зробите ряд керівних принципів, з використанням тих же точок.

Так як ви будете використовувати ряд точок, щоб створити пелюстки та керівні принципи, ви можете зберегти точку значення змінних для повторного використання.

5. Поверніться в текстовому редакторі і додайте наступний код після рядка з пункту 3.

var pt1 = { x: 155, y: 145 };

var pt2 = { x: 93, y: 106 };

var cp1 = { x: 111, y: 154 };

var cp2 = { x: 66, y: 131 };

6. Цей код змінює хід і кольори заливки, а також малює першу пелюстку квітки.

ctx.fillStyle = 'rgb(115,206,226)';

ctx.strokeStyle = 'rgb(0,111,174)';

ctx.beginPath();

ctx.moveTo(pt1.x, pt1.y);

ctx.bezierCurveTo(cp1.x, cp1.y, cp2.x, cp2.y, pt2.x, pt2.y);ctx.bezierCurveTo(89, 65, 159, 118, 155, 145);

ctx.fill();

ctx.stroke();

У перших двох рядках коду змініть окантовку на темно-синій колір і заливку на світло-блакитний колір. Наступні чотири рядки створюють новий шлях за допомогою функції bezierCurveTo для створення гладких кривих.

7. Збережіть HTML-файл, а потім переключіться в браузер і перегляньте HTML-сторінку.

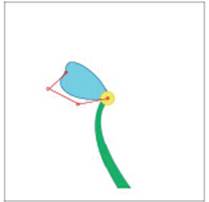
Рисунок 11 – Стовбурова форма з однією квіткою

8. Поверніться до текстового редактора і додайте наступні рядки коду після рядка з попереднього кроку; ці рядки змінять хід і кольори заливки і намалюють центр квітки, пов’язуючи ілюстрації квітки разом:

ctx.fillStyle = 'rgb(243,237,99)';

ctx.strokeStyle = 'rgb(253,183,58)';

ctx.beginPath();

ctx.arc(155, 145, 10, 0, Math.PI * 2, false);

ctx.fill();

ctx.stroke();

9. Щоб уявити собі, як функція bezierCurveTo використовує контрольні точки для визначення кривої, необхідно додати орієнтир, використовуючи ті ж точки, що і перша крива пелюстки квітки. Використовуйте керівні принципи, додаючи наступні рядки коду після рядка з попереднього кроку:

ctx.strokeStyle = 'rgb(255,0,0)';

ctx.beginPath();

ctx.arc(pt1.x, pt1.y, 2, 0, Math.PI * 2, false);

ctx.arc(cp1.x, cp1.y, 2, 0, Math.PI * 2, false);

ctx.arc(cp2.x, cp2.y, 2, 0, Math.PI * 2, false);

ctx.arc(pt2.x, pt2.y, 2, 0, Math.PI * 2, false);

ctx.stroke();

Перший рядок змінює лінію в яскраво-червоний, який виділяється з малюнка квітки. Наступні шість ліній створюють зв’язаний шлях маленьких точок (кіл) в кожній точці.

10. Збережіть HTML-файл, а потім переключіться в браузер і перегляньте HTML-сторінку, що відображає ваші зміни.

Рисунок 12 – Квітка з однією пелюсткою і візуалізації ліній