Перестановкой множества из n элементов называется любой упорядоченный набор из всех элементов этого множества, среди которых нет одинаковых.
Любая транспозиция соседних элементов перестановки меняет четность перестановки на противоположную.
пределение определителя  – го порядка.
– го порядка.
Пусть дана квадратная матрица  – го порядка:
– го порядка:
 .
.
Определение. Произведение  элементов матрицы А, взятых по одному из каждой строки и каждого столбца называют членом определителя матрицы А.
элементов матрицы А, взятых по одному из каждой строки и каждого столбца называют членом определителя матрицы А.
Обозначение:  .
.
Здесь первый индекс обозначает номер строки, из которой взят элемент, второй индекс 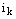 , он в свою очередь имеет нижний индекс
, он в свою очередь имеет нижний индекс  , обозначает номер столбца, из которой взят элемент и набор вторых индексов образует перестановку
, обозначает номер столбца, из которой взят элемент и набор вторых индексов образует перестановку 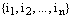 множества
множества  .
.
Т.к. число всех перестановок множества  равно
равно  , то существует ровно
, то существует ровно  членов определителя.
членов определителя.
Каждый член определителя снабдим знаком плюс или минус, в зависимости от четности или нечетности перестановки вторых индексов. Это можно сделать с помощью множителя 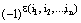 , который равен 1, если перестановка
, который равен 1, если перестановка 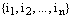 четная и тогда число инверсий
четная и тогда число инверсий  есть четное число и равен – 1, если перестановка
есть четное число и равен – 1, если перестановка 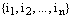 нечетная и тогда число инверсий
нечетная и тогда число инверсий  есть нечетное число.
есть нечетное число.
Определение. Определителем (детерминантом)  – го порядка или определителем (детерминантом) квадратной матрицы
– го порядка или определителем (детерминантом) квадратной матрицы  – го порядка называют алгебраическую сумму всех членов определителя данной матрицы, взятых со своими знаками.
– го порядка называют алгебраическую сумму всех членов определителя данной матрицы, взятых со своими знаками.
Обозначение:

 , (1)
, (1)
где суммирование ведется по всем перестановкам столбцов.
Пример. Вычислим определитель 3 – го порядка:
 .
.
Выпишем все члены определителя, их ровно 6 штук. Для этого, выпишем сначала все перестановки множества из 3 элементов:
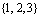 ,
, 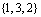 ,
, 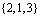 ,
,  ,
,  ,
, 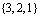 и определим их четность:
и определим их четность:
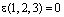 ,
, 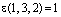 ,
,  ,
, 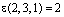 ,
,  ,
, 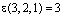 .
.
Теперь выписываем члены определителя, причем первые индексы (номера строк) образуют начальную перестановку, а вторые индексы (номера столбцов) образуют перестановку, одну из 6 приведенных выше.
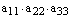 ,
,  ,
, 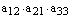 ,
, 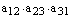 ,
, 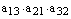 ,
, 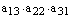 .
.
Теперь мы можем записать определитель, как
алгебраическую сумму всех членов определителей, взятых со знаком плюс, если вторые индексы сомножителей, входящих в член определителя, образуют четную перестановку, и со знаком минус в противном случае:

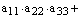

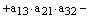
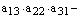

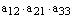 .
.
Замечание. Формула (1) определяет отображение из множества всех квадратных матриц n-го порядка над полем K в полеK. Это отображение называется определителем или детерминантом и обозначается
 .
.
6. Ранг матрицы и способы его вычисления.
7. Определить понятие обратной матрицы и рассказать о способах ее
вычисления.
8. Рассказать о крамеровских системах линейных уравнений и способе
их решения.
9. Раскрыть суть метода Гаусса для решений линейных уравнений общего
вида.
10. Критерий совместности систем линейных уравнений (теорема Кронера-
Капелли).
11. Рассказать о системах однородных линейных уравнений и способе ее
решения. Фундаментальная система решений.
12. Дать определение и привести примеры линейного пространства.
13. Раскрыть понятие линейной зависимости строк и столбцов матрицы.
Ранг матрицы.
14. Определить понятия базиса и размерности линейного пространства.
15. Рассказать о координатах вектора в фиксированном базисе.
16. Раскрыть понятие изоморфизма линейного пространства.
17. Линейные подпространства.
18. Алгебраические операции и их свойства.
19. Алгебраические системы с одной операцией. Примеры.
20. Алгебраические системы с двумя операциями. Примеры.

 – го порядка.
– го порядка. .
. .
.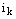 , он в свою очередь имеет нижний индекс
, он в свою очередь имеет нижний индекс  , обозначает номер столбца, из которой взят элемент и набор вторых индексов образует перестановку
, обозначает номер столбца, из которой взят элемент и набор вторых индексов образует перестановку 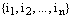 множества
множества  .
. , то существует ровно
, то существует ровно 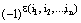 , который равен 1, если перестановка
, который равен 1, если перестановка  есть четное число и равен – 1, если перестановка
есть четное число и равен – 1, если перестановка 
 , (1)
, (1) .
.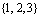 ,
, 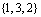 ,
, 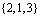 ,
,  ,
,  ,
, 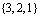 и определим их четность:
и определим их четность: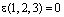 ,
, 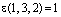 ,
,  ,
, 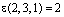 ,
,  ,
, 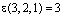 .
.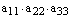 ,
,  ,
, 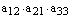 ,
, 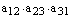 ,
, 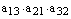 ,
, 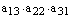 .
.
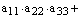

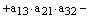
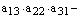

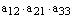 .
. .
. 


