ИДЕНТИФИКАЦИЯ ОБЪЕКТА УПРАВЛЕНИЯ
>> ts=0.2 ts = 0.2000 >> dan=iddata(y(103:302),u(103:302),ts) dan = Time domain data set with 200 samples. Sample time: 0.2 seconds
Outputs Unit (if specified) y1
Inputs Unit (if specified) u1
>> dan.outputn='Температура' dan= Time domain data set with 200 samples. Sample time: 0.2 seconds
Outputs Unit (if specified) Температура
Inputs Unit (if specified) u1
>> dan.inputn='Расход пара' dan = Time domain data set with 200 samples. Sample time: 0.2 seconds
Outputs Unit (if specified) Температура
Inputs Unit (if specified) Расход пара
>> dan.outputUnit='Град Ц' dan = Time domain data set with 200 samples. Sample time: 0.2 seconds
Outputs Unit (if specified) Температура Град Ц
Inputs Unit (if specified) Расход пара
>> dan.inputUnit='м3/час' dan = Time domain data set with 200 samples. Sample time: 0.2 seconds
Outputs Unit (if specified) Температура Град Ц
Inputs Unit (if specified) Расход пара м3/час
>> get(dan) ans = Domain: 'Time' Name: '' OutputData: [200x1 double] y: 'Same as OutputData' OutputName: {'Температура'} OutputUnit: {'Град Ц'} InputData: [200x1 double] u: 'Same as InputData' InputName: {'Расход пара'} InputUnit: {'м3/час'} Period: Inf InterSample: 'zoh' Ts: 0.2000 Tstart: [] SamplingInstants: [200x0 double] TimeUnit: 'seconds' ExperimentName: 'Exp1' Notes: {} UserData: []
>> plot(dan) >> ident >> [num,den]=th2tf(arx441) num = 0 0.0017 -0.0017 0.0637 0.0646 den = 1.0000 -0.9798 -0.1284 0.3135 -0.0663 num = 0 0.0017 -0.0017 0.0637 0.0646 den = 1.0000 -0.9798 -0.1284 0.3135 -0.0663 >> WZ=tf(num,den,ts)
WZ = 0.001701 z^3 - 0.001731 z^2 + 0.06368 z + 0.06463 -------------------------------------------------- z^4 - 0.9798 z^3 - 0.1284 z^2 + 0.3135 z - 0.06625
Sample time: 0.2 seconds Discrete-time transfer function.
>> WS=d2c(WZ)
WS = 1.002 s^4 - 4.842 s^3 + 215.8 s^2 - 1664 s + 7058 ------------------------------------------------------ s^5 + 16.38 s^4 + 349.6 s^3 + 2963 s^2 + 8923 s + 7649
Continuous-time transfer function. >> step(WS,WZ) >> impulse(WS,WZ) >> bode(WS,WZ) >>nyquistplot(WS,WZ)
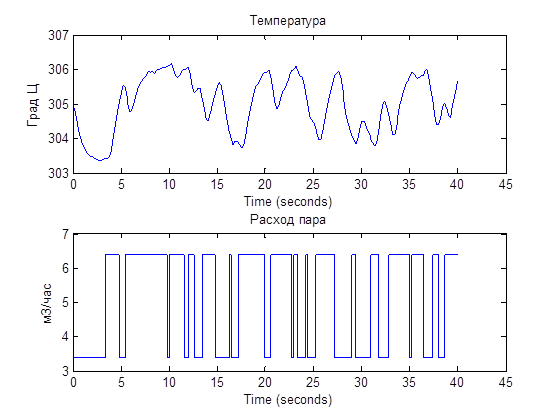
Рисунок 4 – Исходные данные для идентификации ТОУ
Рисунок 5 – Графики переходных процессов модели WS и WZ На графиках переходных процессов ступенчатой линией представлен переходной процесс дискретной модели, а сплошной линией – непрерывной модели. Кроме того, в поле графика указаны основные характеристики переходного процесса: • время нарастания переходного процесса (Rise time) – 1,76 с для обоих моделей; • время регулирования (Setting time) – 2,9 для непрерывной модели и 2,89 с для дискретной модели; • установившееся значение выходной координаты (Final value) – 0,923 для обоих моделей.
Рисунок 6 – Графики импульсной характеристики Основными характеристиками модели ТОУ при подаче на вход единичного импульсного воздействия являются: • пиковая амплитуда (Peak amplitude) составляет для дискретной модели 0,662, а для непрерывной – 1. • время регулирования составляет для дискретной модели 4,12 с, а для непрерывной модели – 3,72 с.
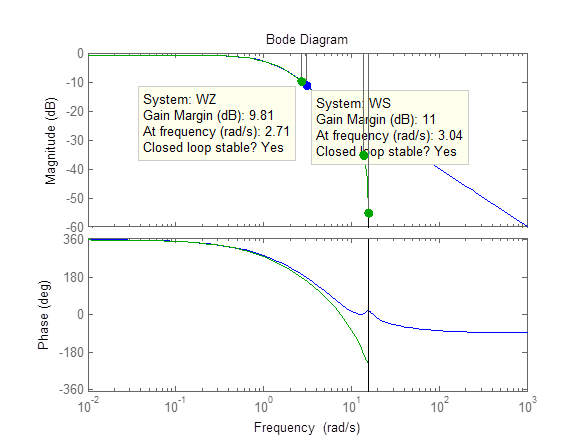
Рисунок 7 – Частотные характеристики моделей
На графиках частотных характеристик указаны значения запасов устойчивости по амплитуде (Gain Margin), которые для дискретной модели составляет 9,81 dB, а для непрерывной модели – 11 dB.
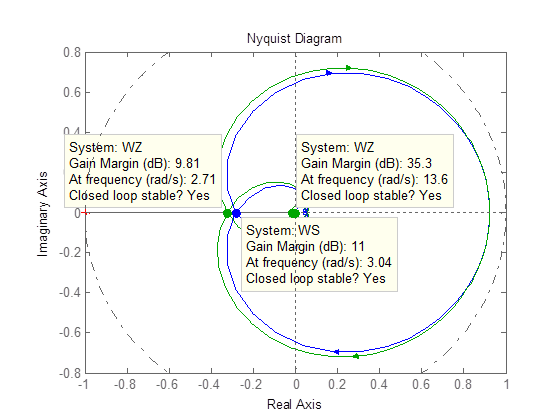
Рисунок 8 – Годограф АФХ с указанием значений запасов устойчивости для непрерывной и дискретной моделей
Анализ частотных характеристик показывает, что модели WZ и WS являются устойчивыми с соответствующими запасами устойчивости по амплитуде. Запас устойчивости по фазе равен бесконечности. Этот вывод подтверждается так же комплексной амплитудно-фазовой характеристикой АФХ, которая в зарубежной литературе называется диаграммой Найквиста, так как годограф АФХ не пресекает точку комплексной плоскости с координатами –1, j0.
|