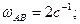ВВЕДЕНИЕ. Данные методические указания содержат краткую теорию и решение типовых примеров на исследование плоскопараллельного движения многозвенного механизма
Данные методические указания содержат краткую теорию и решение типовых примеров на исследование плоскопараллельного движения многозвенного механизма. Рекомендуется пользоваться следующей литературой: 1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т.I.-M.: Наука, 1980. 2. Тарг С.М. Краткий курс теоретической механики. –М.: Физматгиз, 1963 и последующие издания. 3. Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. –М.: Высшая школа, 1966. 4. Лойцанский Л.Г., Лурье А.И. Курс теоретической механики. Ч.II.-M.: Наука, 1983.
1. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Определение. Плоскопараллельным называется такое движение твердого тела, при котором расстояние от любой точки тела до некоторой неподвижной плоскости остается неизменным. Примеры: I. Качение колеса по неподвижной поверхности (рис.I);
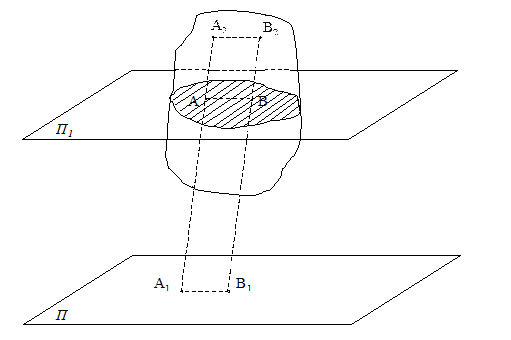
Покажем, что при таком движении точки тела, расположенные в данный момент времени на одном и том же перпендикуляре к неподвижной плоскости, остаются и в любой момент движения на перпендикуляре к ней (рис.3).
Рис.3 Пусть твердое тело совершает плоское движение, параллельное неподвижной плоскости П. Возьмём произвольную точку А2 данного тела и опустим из не перпендикуляр на неподвижную плоскость П. А1 – точка пересечения этого перпендикуляра с плоскостью П, то есть А2А1┴пл.П. Пусть через произвольный промежуток времени точка А2 перейдет в новое положение В2 точка А1 в В1. Надо показать, что В2В1┴пл.П. Из определения абсолютно твердого тела следует, что А2А1=В2В1. Из определения плоского движения вытекает, что А2В2┴А2А1 и А1В1┴А2А1, а также, что А2В2║пл.П и А1В1║пл.П. Отсюда следует, что А2В2║А1В1, так как в противном случае В2В1> А2А1. Поэтому полученная фигура А1А2В2В1 – прямоугольник и В2В1┴пл.П, что и требовалось показать. Вывод. Любая прямая, перпендикулярная к этой неподвижной плоскости и жестко соединенная с движущимся телом, будет двигаться поступательно. Таким образом, для изучения движения точек, лежащих на рассматриваемой прямой, достаточно рассмотреть движение любой точки этой прямой, например точки А. Для изучения движения точек этого тела достаточно рассмотреть движение точек, лежащих в плоскости неподвижной плоскости, например пл.П1║пл.П, то есть точек, лежащих в сечении рассматриваемого тела плоскостью П1 (рис.3). Таким образом, для изучения плоского движения твердого тела достаточно изучить движение сечения, параллельного неподвижной плоскости П.
2. УРАВНЕНИЕ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Проведем сечение S тела (рис.4) и свяжем с телом подвижную систему координат x1cy1. Введем неподвижную систему координат xoy, относительно которой рассмотрим движение сечения S.
Рис.4 Для того чтобы в любой момент времени знать положение сечения S, достаточно показать положение любого отрезка см, проведенного в этом сечении. Положение отрезка см относительно системы координат xoу можно определить, задав координаты какой-либо точки этого отрезка и его направление. Например, для точки С нужно задать координаты хс, ус , а направление указать углом φ;, между любой осью или отрезком см и осью ох. Таким образом, уравнения движения плоской фигуры в ее плоскости, а следовательно, и плоского движения твердого тела относительно системы координат xoу имеют вид: xс = f1 (t); yс = f2 (t); (1) φ = f3 (t). Рассмотрим частные случаи: 1. Из формул (1) следует, что если φ = const, то изменяются xс = f1 (t); yс = f2 (t). (2) (2) – уравнения поступательного движения. 2. Пусть xc=const, yc=const, то из уравнений (1) вытекает, что φ = f3 (t). (3) (3) – уравнения вращательного движения вокруг оси, проходящей через точку С, называемую полюсом. Вывод. Поступательное и вращательное движения есть частные случаи плоского движения. Плоское движение можно рассматривать как сумму этих движений.
3. ТЕОРЕМА ШАЛЯ
Всякое непоступательное перемещение плоской фигуры в плоскости можно осуществить одним поступательным перемещением вместе с произвольно выбранным полюсом и одним вращением вокруг оси, проходящей через этот полюс.
Рис.5 Рассмотрим движение фигуры в плоскости хоу. Пусть в начальный момент времени t она занимает положение I, определяемое отрезком АВ (рис.5). В конечный момент фигура находится в положении II. Покажем, что из I во II положение её можно перевести двумя способами, выбирая за полюс либо точку В или точку А, при этом углы поворотов φ и φ1 равны. I способ: из положения I фигуру поступательно переместим в положение III, а затем вращением вокруг А1 она займёт положение II. 2 способ: из положения I переместим фигуру поступательно в положение IУ и повернём вокруг точки В1 по ходу вращения часовой стрелки в положение II. Вывод. Поступательная часть плоского перемещения зависит от выбора полюса, а вращательная не зависит от него.
4. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКОГО ДВИЖЕНИЯ
Кинематическими характеристиками движения плоской фигуры являются линейные скорости ω = φ =
причем ω, ε, на основании теоремы Шаля, не зависят от выбора полюса. При плоском движении тела угловую скорость и угловое ускорение можно считать векторами, направленными по подвижной оси, перпендикулярно к плоскости фигуры и проходящей через выбранный полюс. Вектор угловой скорости Вектор
Рис.6
5. ОПРЕДЕЛЕНИЕ СКОРОСТИ ТОЧЕК ПЛОСКОЙ ФИГУРЫ Скорости точек плоской фигуры можно определить тремя способами. 5.1. Разложение плоского движения на переносное и относительное. Рассмотрим плоское движение тела как сложное. Тогда абсолютную скорость любой его точки В по теореме о сложении скоростей можно представить в виде рис.7, где
Учитывая, что
Обозначим
Формула (5) показывает, что скорость относительного движения точки В получается от вращения плоской фигуры вокруг подвижной оси, проходящей через точку А, или просто вокруг точки А. Формулу (4) можно представить в виде:
где VB/A = ωAB. (7) Вывод. Скорость любой точки фигуры при её плоском движении равна векторной сумме скорости полюса и относительной скорости этой точки от вращения фигуры вокруг полюса.
Пример. Колесо радиуса R (рис.8) катится со скольжением по прямой линии с угловой скоростью ω, имея в рассматриваемый момент скорость центра  . Найти в этот момент величины скоростей точек М, К, N, лежащих на концах вертикального и горизонтального диаметров. . Найти в этот момент величины скоростей точек М, К, N, лежащих на концах вертикального и горизонтального диаметров.
Решение. В качестве полюса выберем точку 0, в которой известны величина и направление скорости
VM/0 =ω OM = ωR. Так как VM = V0 + VM/0. Для точки К скорости VK = V0 – VK/o, где VK/o= ωR. В точке N скорости
где VN/0 = ωON = ωR. 5.2. Нахождение скоростей точек плоской фигуры с помощью теоремы о проекциях скоростей Теорема. Проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны. Дано: углы α, β. Доказать, что ПРАВ Доказательство. Примем одну из точек плоской фигуры (например точку А) за полюс (рис.9), тогда по формуле (6):
 = =  + + 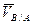 (8) (8)
В равенстве (8):
Спроецируем векторное равенство (8) на направление отрезка АВ: ПРАВ Так как
Тогда имеем: ПРАВ или VB cosβ = VA cosα. (9) В силу того, что точки А, В были взяты произвольно, равенство (9) справедливо для любых точек плоской фигуры, что и требовалось доказать. 5.3. Метод мгновенных центров скоростей Определение. Мгновенным центром скоростей (М.Ц.С.) плоской фигуры называется неизменно связанная с ней точка, скорость которой в данный момент времени равна нулю. Теорема. При непоступательном движении плоской фигуры всегда существует в плоскости ее движения М.Ц.С. и притом единственный. Дано. Уравнения движения полюса А: хА = f1(t), УА = f2(t), φ = f3(t). Доказать: 1. Существование точки, скорость которой равна нулю. 2. Единственность такой точки. Доказательство. 1. По условию известно, что скорость полюса VA ≠ 0 иугловая скоростьω ≠ 0 (рис.10). На перпендикуляре к вектору VA выберем точку Р на расстоянии АР =
Тогда на основании формулы (6) можно записать, что:
Причем: Из формулы (7) следует, что
Подставляя в (11) выражение (10), получим
следовательно,
то есть абсолютная скорость точки Р равна нулю: VР = 0. Таким образом, доказали первую часть теоремы, что всегда можно найти точку в плоскости движения фигуры, скорость которой в данный момент времени равна нулю, то есть Р – М.Ц.С. 2. Для доказательства единственности М.Ц.С. предположим, что существует ещё точка Р1, абсолютная скорость которой VР1 = 0 (рис.10). Выберем в качестве полюса точку Р, тогда на основании формулы (6) имеем:
учитывая, что
По предложению VР1 = 0, следовательно, ω РР1 = 0, так как ω ≠ 0, имеем РР1 = 0, то есть точки Р и Р1 совпали, что и требовалось доказать. 5.3.1. Свойства мгновенного центра скоростей
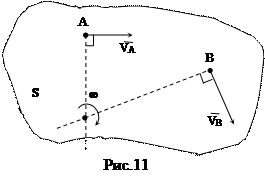
1. Скорость любой точки тела, лежащей в сечении S, равна ее вращательной скорости вокруг М.Ц.С. (рис.11).
Действительно, если в качестве полюса выбрать точку Р – М.Ц.С., то из формул (6), (7) следует, что скорость произвольной точки плоской фигуры можно определить по формуле:
где РВ и РА расстояния от М.Ц.С. Р до точек В и А соответственно. Таким образом, скорости всех точек плоской фигуры будут такими, как если бы в данный момент фигура вращалась вокруг оси, проходящей через М.Ц.С. 2. Скорости точек тела пропорциональны их расстояниям до М.Ц.С. Из равенств (12) следует, что
3. Угловая скорость тела равна в каждый данный момент времени отношения скорости какой-нибудь точки плоской фигуры к ее расстоянию от М.Ц.С. Это свойство следует из формул (12).
4. Для определения скорости любой точки тела надо знать модуль и правление скорости какой-нибудь одной точки А тела и направление скорости другой его точки В. Из равенств (13) следует, что зная скорость VA, можно определить скорость VB. По направлению вектора 5.3.2. Определение положения мгновенного центра скоростей Существует два способа нахождения М.Ц.С. 1. М.Ц.С. находится из механических условий задачи, то есть сразу удается указать точку плоскости фигуры, скорость которой в рассматриваемый момент времени равна нулю. Пример: Качение без скольжения одного тела по неподвижной поверхности другого. Точка касания таких двух тел и будет М.Ц.С. (рис.12).
2. Для нахождения М.Ц.С. нужно знать только направления скоростей  и и 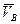 каких-нибудь двух точек А и В плоской фигуры. М.Ц.С. находится в точке пересечения перпендикуляров, восстановленных из точек А и В в скоростях этих точек (рис.11). В 5.3. было доказано, что М.Ц.С. лежит на перпендикуляре к скорости. Восстановив перпендикуляры к двум заданным скоростям каких-нибудь двух точек А и В плоской фигуры. М.Ц.С. находится в точке пересечения перпендикуляров, восстановленных из точек А и В в скоростях этих точек (рис.11). В 5.3. было доказано, что М.Ц.С. лежит на перпендикуляре к скорости. Восстановив перпендикуляры к двум заданным скоростям  , , 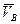 , получим единственную точку их пересечения – Р, которая и будет М.Ц.С. , получим единственную точку их пересечения – Р, которая и будет М.Ц.С.
Пример. Колесо радиуса R катится без скольжения по горизонтальной неподвижной поверхности (рис.13). Скорость центра колеса V0. Найти скорости точек А, В, D, лежащих на концах вертикального и горизонтального диаметров.
Дано. Скорость центра колеса V0 . Найти. Скорости VA, VB, VD. Решение. Так как колесо движется без скольжения, то скорость точки касания с неподвижной поверхностью равна нулю, то есть точка Р – М.Ц.С. Применяя формулу (12), получим:
Учитывая, что точка Р – М.Ц.С. запишем для точек VA, VB, VD соответственно:
5.3.3. Частные случаи определения мгновенного центра скоростей 1. Известно, что
Из теоремы о проекциях скоростей следует, что ПРАВ VA cos α = VB cos α;. Так как cosα ≠ 0, то VA = VВ Аналогичный результат получается для всех других точек тела. Примем за полюс точку А, тогда по формуле (6)
Учитывая равенство (15), получим, что VB/A = 0, но VB/A = ωАВ = 0, следовательно, ω= 0. Возьмём произвольную точку D. Принимая точку А за полюс, имеем:
где VD/A = ωAD, Учитывая, что ω = 0, получим VD/A = 0. Таким образом,
Так как точка D была взята произвольно, следовательно, скорости любых точек плоской фигуры равны по величине и одинаково направлены. Движение плоской фигуры в этом случае называется мгновенно поступательным и М.Ц.С. находится в бесконечности (рис.15).
2. Скорости точек А и В тела параллельны друг другу и при этом линия АВ перпендикулярна к
Рис.16 М.Ц.С. определяется построениями, показанными на рис.16. Справедливость построений вытекает из формул (13). Пример. В кривошипно-шатунном механизме кривошип ОА длиной r = 40см вращается с угловой скоростью
Рис.17 Дано: ОА =r = 40cм; ω;0 = 6πс-1; АС = СВ; φ = 600 ; ОА┴АВ. Найти: ω – угловую скорость шатуна АВ. VB, Vc – скорости точек В и С. Решение. Определим неизвестные величины с помощью М.Ц.С. Для нахождения М.Ц.С. шатуна АВ изобразим на чертеже (рис.17) векторы скоростей двух точек А и В. Рассматривая эти точки принадлежащими другим звеньям механизма, а именно: кривошипу ОА, вращающемуся вокруг оси, проходящей через точку О, и ползуну В находятся легко, а именно: Модуль скорости точки А, как точки кривошипа ОА, равен VA = ω0r. С другой стороны, модуль скорости этой же точки как точки шатуна АВ будет VA = ωAP, где ω – угловая скорость шатуна АВ. Следовательно, ω = или ω = Скорости точек В и С соответственно VB = ωBP, Vс = ωСР, (17) причем Рассматривая треугольники ОАВ и ОРВ найдём:
Подставляя найденные значения в формулы (16), (17), получим:
6. УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
Пусть фигура S участвует в плоском движении (рис.18).
Будем рассматривать плоское движение как сложное.
По теореме о сложении ускорений, абсолютное ускорение произвольной точки В можно представить в виде:
Кориолисово ускорение
Окончательно формула (18) принимает вид:
где
Вывод. Ускорение произвольной точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг этого полюса. Пример. Кривошип ОА длины 20 см вращается равномерно с угловой скоростью
Рис.19
Дано: ОА = 0,2 м; Найти: ωАВ – угловую скорость шатуна АВ; εАВ - угловое ускорение шатуна АВ; αВ – ускорение точки В. Решение. Пусть точка А полюс, тогда рассматривая ее принадлежащей вращающемуся кривошипу ОА, определим ее скорость
где
Так как ε0 = ω0 = 0 (ω0 = const). Посмотрим М.Ц.С. для шатуна АВ – точку Р. Угловая скорость шатуна АВ ωАВ = Ускорение точки В определим по формуле (20):
причем
Спроецируем равенство (21) на оси х, у.
Решая полученную систему, находим:
Ответ:
Редактор Н.Е.Гладких Темплан 2006г., поз.168 Подписано в печать 29.06.06 Формат 60х84/16. Ризограф. Бумага писчая. Уч.-изд. л. 1,3. Тираж 50 экз. Заказ 603. __________________________________________________________________ Редакционно-издательский центр Ростовского государственного строительного университета 344022, Ростов-на-Дону, ул. Социалистическая, 162
|

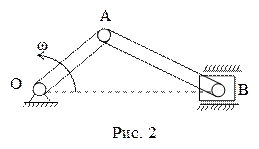 2. Движение шатуна АВ кривошипно-шатунного механизма (рис.2).
2. Движение шатуна АВ кривошипно-шатунного механизма (рис.2).


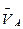 и ускорение
и ускорение  поступательно движущегося полюса А, угловая скорость ω и угловое ускорение ε вращения этого тела вокруг оси, проходящей через полюс, перпендикулярно плоскости фигуры. Остановимся подробнее на понятиях ω и ε. Если угол поворота вокруг подвижной оси обозначить φ, то
поступательно движущегося полюса А, угловая скорость ω и угловое ускорение ε вращения этого тела вокруг оси, проходящей через полюс, перпендикулярно плоскости фигуры. Остановимся подробнее на понятиях ω и ε. Если угол поворота вокруг подвижной оси обозначить φ, то ; ε =
; ε = 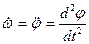 ;
; при плоском движении фигуры направлен по подвижной оси так, чтобы с его конца видеть вращение фигуры против хода часовой стрелки.
при плоском движении фигуры направлен по подвижной оси так, чтобы с его конца видеть вращение фигуры против хода часовой стрелки. при ускоренном вращении фигуры совпадает с направлением вектора угловой скорости
при ускоренном вращении фигуры совпадает с направлением вектора угловой скорости  векторами.
векторами. - скорость точки В от переносного поступательного движения фигуры;
- скорость точки В от переносного поступательного движения фигуры; - скорость точки В в относительном движении, которым является вращение плоской фигуры вокруг точки А с угловой скоростью ω.
- скорость точки В в относительном движении, которым является вращение плоской фигуры вокруг точки А с угловой скоростью ω.
 = ωAB, где
= ωAB, где  направлен по подвижной оси вращения, проходящей через точку А и перпендикулярной к плоскости фигуры.
направлен по подвижной оси вращения, проходящей через точку А и перпендикулярной к плоскости фигуры. . (5)
. (5)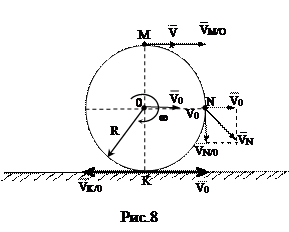

 противоположны по направлению
противоположны по направлению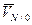 перпендикулярны, поэтому
перпендикулярны, поэтому ,
,
 АВ.
АВ. = ПРАВ
= ПРАВ  . (10)
. (10)
 .
.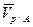
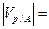 ω АР. (11)
ω АР. (11)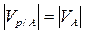 ;
; ;
; ;
; , получим
, получим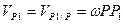 .
.
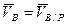 ,
,  VB = ω PB;
VB = ω PB; , VA = ω PA, (12)
, VA = ω PA, (12)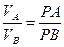 . (13)
. (13)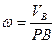 . (14)
. (14) . Скорость любой другой точки фигуры можно определять далее по формуле (12).
. Скорость любой другой точки фигуры можно определять далее по формуле (12).





 ||
|| 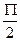 (рис.14)
(рис.14)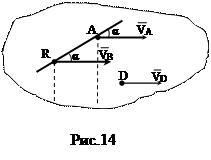
 .
. ,
, VD = VA.
VD = VA.

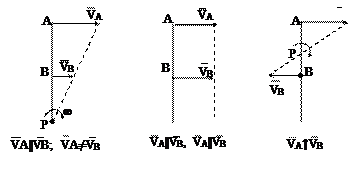
 . Определить скорости ползуна В и средней точки С шатуна АВ, а также его угловую скорость ω в момент времени, когда ОА и АВ взаимно перпендикулярны и φ = 600 (рис.17).
. Определить скорости ползуна В и средней точки С шатуна АВ, а также его угловую скорость ω в момент времени, когда ОА и АВ взаимно перпендикулярны и φ = 600 (рис.17).
 ┴ОА,
┴ОА,  - направление вдоль ОВ. Восстанавливая перпендикуляры к векторам скоростей
- направление вдоль ОВ. Восстанавливая перпендикуляры к векторам скоростей  (16)
(16) . (16а)
. (16а)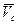 ┴СР.
┴СР.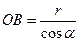 ,
, 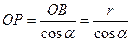 ;
;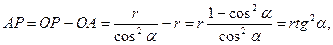

 ;
; ;
; 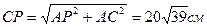 ;
; 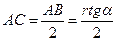 .
.

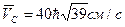 .
.
 (18)
(18) так как тело движется поступательно относительно неподвижной системы координат хоу. Примем за полюс произвольную точку А плоской фигуры S. Так как переносное движение точки В – это поступательное движение плоской фигуры с ускорением полюса А, то
так как тело движется поступательно относительно неподвижной системы координат хоу. Примем за полюс произвольную точку А плоской фигуры S. Так как переносное движение точки В – это поступательное движение плоской фигуры с ускорением полюса А, то  . Учитывая, что относительное движение точки В – есть вращение этой точки вместе с плоской фигурой S вокруг оси, проходящей через полюс А перпендикулярно к плоскости фигуры, получим:
. Учитывая, что относительное движение точки В – есть вращение этой точки вместе с плоской фигурой S вокруг оси, проходящей через полюс А перпендикулярно к плоскости фигуры, получим: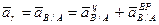 . (19)
. (19) , (20)
, (20)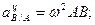
 (21)
(21) , приводит в движение шатун АВ длины 100 см; ползун В движется по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также ускорение ползуна В в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью углы
, приводит в движение шатун АВ длины 100 см; ползун В движется по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также ускорение ползуна В в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью углы  (рис.19)
(рис.19)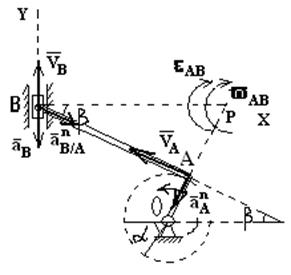
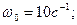 АВ = 1 м; α = β = 450.
АВ = 1 м; α = β = 450. и ускорение
и ускорение 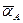 по формулам:
по формулам: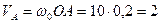 м/с;
м/с; ,
,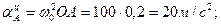
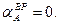
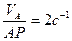 .
. ; (21)
; (21)



 ;
;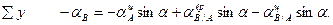

 ;
;