Теорема 2.3
Произведение ограниченной функции и функции, бесконечно малой в точке a, является бесконечно малой в точке a функцией. Доказательство: Тогда " e > 0 $ d > 0: " x Î {0 < | x - a | < d }: | g (x) | < Следовательно, " x Î {0 < | x - a | < d }: | f (x) g (x) | = Теорема доказана. Следствие. Произведение конечного числа ограниченных функций, из которых хотя бы одна - бесконечно малая в точке а, является бесконечно малой функцией в точке а.
Сравнение бесконечно малых и бесконечно больших функций. Пусть f (x) и g (x)- бесконечно малые в точке а, то есть Тогда Если Примеры:
Эти два неравенства, как и вообще неравенства с символом 0-малое, верны только слева направо, так как символ 0(х) обозначает любую функцию, являющуюся бесконечно малой более высокого порядка, чем х, при x ® 0. Если
Пример:
Если Обозначение: f ~ g при x ® 0.
Пример:
Свойства символа "0 малое": 1) 0(g) ± 0(g) = 0(g). 2)Если f = 0(g), то 0(f) ± 0(g) = 0(g). 3) fg = 0(f), fg = 0(g). 4)Если f ~ g, то f - g = 0(f), f - g = 0(g). 5)Если с = const ¹ 0, то 0(cg) = 0(g), например, 0(5 Докажем 2): Для этого нужно доказать, что
а это и означает, что 0(f) ± 0(g) = 0(g), что и требовалось доказать.
Докажем 4): Для этого нужно доказать, что
Пусть f (x) и g (x) - бесконечно большие функции при x ® а. Тогда Если Пример: f(x)=
Если Другие типы неопределённостей: ¥ - ¥: например, 0 × ¥: например, xctgx при x ® 0;
5 Свойства пределов функций.
Лемма 1: Если Доказательство: Запишем функцию f (x) в виде f (x) = b + Остаётся доказать, что a(x) = f (x) - b - бесконечно малая в функция в точке a. По определению предела функции, " e > 0 $ d > 0, " x Î {0 < | x - a | < d }: | f (x) - b | < e. То есть | a(x) | < e. Это и означает по определению, что a(x) - бесконечно малая функция в точке а. Лемма 1 доказана. Лемма 2 (обратная лемме 1): Если f(x) = b + a(x), где b -число, a(x)-бесконечно малая функция в точке а. то Доказать самостоятельно. Теорема 2.4 Пусть функции f (x) и g (x) определены в некоторой проколотой окрестности точки а и пусть Тогда: 1) 2) 3) Если с ¹ 0, то в некоторой проколотой окрестности точки а определена функция Доказательство. 1.Докажем для суммы. Согласно лемме 1, f (x) и g (x) можно представить в виде: f (x) = b + a(x), g (x) = c + b(x), где a(x) и b(x)- бесконечно малые функции в точке а. f (x) + g (x) = (b + c) + [a(x) + b(x)]. Отсюда по лемме 2 следует, что Утверждение 1 для суммы доказано. Докажем 3. Пусть для определённости c > 0. Возьмём e = $ d > 0, " x Î {0 < | x - a | < d }: | g (x) - c | < e = Из пдчеркнутого неравенства следует что g (x) > Так как малая в точке а, то Итак, Следовательно, по лемме 2, Утверждение 3) доказано. Утверждение 2) доказывается таким же образом. Теорема доказана. Теорема 2.4 верна также для пределов функций при х ® ¥. Следствие 1.
Следствие 2. Пусть Доказательство: Пусть Отсюда в силу теоремы 2.4 следует:
Аналогично, Теорема 2.5 Если f (x) ³ с (£ с), и Доказательство: Рассмотрим случай, когда f (x) ³ c. Допустим, что b < c. Возьмём e столь малым, чтобы b + e < c. Согласно определению предела функции, в некоторой проколотой окрестности точки a все значения f (x) будут принадлежать (b - e, b + e), и, тем самым, будут < c, что противоречит условию f (x) ³ с. Полученное противоречие доказывает, что b ³ c. Теорема доказана. Замечание 1: Теорема 2.5 верна также для предела функции при x ® ¥. Замечание 2: Из неравенства f(x) > с, не следует, что lim f(x) > с, а следует лишь, что lim f(x) ³ с. Пример: f(x) =
Замечание 3: Применяя теорему 2.5 к числовым последовательностям, приходим к следующему утверждению: Если " n: a £ Теорема 2.6 (о двух милиционерах). Если f (x) £ g (x) £ h (x), и Доказательство: зададим произвольное e > 0. По определнию предела функции, $ d >0, " x Î {0 | x - a | < d}: | f(x) - b | < e, | h(x) - b | < e. (1) Из условия теоремы следует, что f(x) - b £ g(x) - b £ h(x) - b, и поэтому, в силу неравенства (1) имеем: | g (x) - b | < e " x Î {0 | x - a | < d}, а это и означает, что Теорема доказана.
|

 .
. ×
×  < e. Это и означает по определению, что f (x) g (x)- бесконечно малая в точке а функция.
< e. Это и означает по определению, что f (x) g (x)- бесконечно малая в точке а функция. f (x) = 0,
f (x) = 0,  называют неопределенностью типа
называют неопределенностью типа 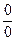 .
.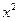 =0(x) при x ® 0,
=0(x) при x ® 0, =0(x) при x ® 0.
=0(x) при x ® 0.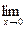
 =
=  =
= 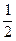 ¹ 0.
¹ 0. = 0.
= 0. +
+  =
= 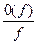 ×
×  +
+  ×
× 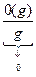 +
+  = 0.
= 0. ® 0, при х ® а, а это и означает, что f - g = 0(f), при х ® а.
® 0, при х ® а, а это и означает, что f - g = 0(f), при х ® а. .
. и g (x) =
и g (x) = 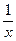 - бескончно большие при x ® 0. Так как
- бескончно большие при x ® 0. Так как  : например,
: например,  при x ® 0;
при x ® 0; : например,
: например,  при x ® + 0;
при x ® + 0; : например
: например  ,при x ® +¥.
,при x ® +¥. .
. (то есть g (x) ¹ 0) и
(то есть g (x) ¹ 0) и  =
= 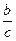 .
. , тогда по определению предела функции
, тогда по определению предела функции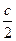 ., или
., или  <
<  -
-  (с a(x)- b b(x)).
(с a(x)- b b(x)). <
< 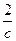 в проколотой d- окрестности точки а и с a(x)- b b(x) бесконечно
в проколотой d- окрестности точки а и с a(x)- b b(x) бесконечно (x) и
(x) и  (х) - многочлены степени n и m. Функция f (x) =
(х) - многочлены степени n и m. Функция f (x) = 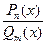 называется рациональной функцией. Утверждение: если
называется рациональной функцией. Утверждение: если  .
.
 +
+ 
 +…+
+…+  , где
, где  f(x) = 0.
f(x) = 0. £ b (то есть
£ b (то есть 


