Бесконечно малые и бесконечно большие функции. Эквивалентное определениеФункция f (x) называется бесконечно малой в точке x = a (при x ® a), если Эквивалентное определение: f(x) называется бесконечно малой в точке a, если " e > 0 $ d > 0, " x Î {0 < | x - a | < d }: | f (x) | < e. Примеры: 1) f (x)=sin x бесконечно малая в точке x = 0, т.к. 2) f (x)=sgn x не является бесконечно малой в точке x = 0, хотя f (0) = 0. Аналогичным образом определяется бесконечно малая функция при x ® ¥ (+¥ или -¥). Пример. f (x) = В частности, последовательность { Функция f (x) называется бесконечно большой в точке x = a (при x ® a), если " A > 0 $ d > 0, " x Î {0 < | x - a | < d }: | f (x) | > A. Обозначение: Если при этом функция принимает положительные (отрицательные) значения, то будем писать:
Пример: f (x) = Докажем, что Зададим произвольное A > 0 и возьмём d = " x Î {0 < | x | < d = это и означает, по определению, что (рисунок)
Задание: Дать определения, выражаемые следующими символическими формулами:
Дома: Доказать следующие утверждения: 1) Если f (x) - бесконечно большая функция в точке x = a, то в некоторой проколотой окрестности точки a определена функция g (x) = 2) Если f (x) - бесконечно малая в точке х = a и в некоторой проколотой окрестности точки a f (x) ¹ 0, то g (x) = 3) Если f (x) = c = const и f(x) - бесконечно малая в точке x = a, то c = 0.
|
f(x) = 0.
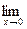sin x = 0.
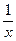- бесконечно малая при x ® ¥.
} называется бесконечно малой, если lim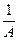 
, тогда
= 
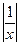> A,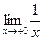
= + ¥.
= - ¥.
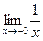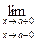f (x) = ¥, + ¥, - ¥.
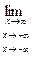f (x) = ¥, + ¥, - ¥.
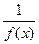и она является бесконечно малой в точке x = a.
