Определение непрерывности, точки разрыва функции.
Определение 1: Пусть f (x) определена в некоторой окрестности точки а. f (x) называется непрерывной в точке а если Примеры: f (x) = sin x непрерывна в точке х =0, так как Рациональная функция f (x) = так как было доказано, что Замечаение: Так как
Таким образом, непрерывность f (x) в точке а означает, что символы Определение 2. f (x) называетмя непрерывной в точке а, если " e > 0 $ d > 0: | f (x) - f (а) | < e при | х - а | < d. Пусть f (x) непрерывна в точке а и f (а) > 0. Возьмём e = f (a). По определнию 2 $ d > 0: | f (x) - f (a) | < f (а) при | х - а | < d, то есть - f ( a ) < f ( x ) - f ( a ) < f (a) в d- окрестности точки а. Из последнего неравенства следует, что f (x) > 0 в d- окрестности точки а. Итак, если f (x) положительна и непрерывна в точке а, то она остается положительной в некоторой окрестности точки а. Это свойство называется устойчивостью знака непрерывной функции. Пусть f (x) определена на [ a, a + d). Функция f (x) называется непрерывной в точке а справа, если Аналогично определяется непрерывность в точке а слева. Пример: f (x) = [ x ]. (рисунок) " целого n: f (n - 0) = n - 1, f (n + 0) = n, f (n) = n, то есть, f (n + 0) = f (n) ¹ f (n - 0). Следовательно, в целочисленных точках эта функция непрерывна только справа. В остальных точках- и справа и слева.
|

 f (x) = f (а)
f (x) = f (а)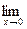 sin x = 0, и sin 0 = 0, то есть
sin x = 0, и sin 0 = 0, то есть 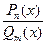 непрерывна в любой точке а, в которой
непрерывна в любой точке а, в которой  (а) ¹ 0,
(а) ¹ 0, (
(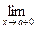 f (x) = f (а). (то есть f (а + 0) = f (а)).
f (x) = f (а). (то есть f (а + 0) = f (а)).


