Умножение
1)Пусть x > 0 и y > 0 - произвольные вещественные числа и пусть xr и yr- любые рациональные числа, удовлетворяющие неравенствам: 0 < xr £ x, 0 < yr £ y. Рассмотрим множество {xr yr}, где умножение производится по правилу для рациональных чисел. Оно ограниченно сверху и поэтому имеет точную верхнюю грань. По определению xy = 2) " x: x ×0 = 0× x = 0. 3) если x ¹ 0, y ¹ 0, то xy =
Вычитание и деление вещественных чисел вводятся как операции, обратные сложению и умножению. Разность x и y - это вещественное число z, такое, что z + y = x. Можно доказать, что " x и y разность $ и единственна. Частное от деления x на y ¹ 0 - это вещественное число z, такое, что zy = x. Можно доказать, что " x и y ¹ 0 частное существует и единственно. 3 Понятие функции. Определение предела функции. Пусть Х - числовое множество. Если каждому х Î Х поставлено в соответствие некоторое (единственное) число y, то говорят что на множестве Х определена (задана) функция и пишут y = f (x), x Î X. Множество X называется областью определения функции, х - аргументом функции или независимой переменной. Число у, соответствующее данному х, называется частным значением функции в точке х, а множество { y } = Y, называется множеством значений функции. Пусть X - числовое множество. Число a (a Î X, либо a Ï X) называется предельной точкой множества X, если в " окрестности точки a содержатся точки (хотя бы одна) из множества X, отличные от а: x Î X, x ¹ a. Пример 1: X = (a < x < b) " точка из (a, b) а также точки a и b - предельные точки X. Все остальные точки не являются предельными точками X. Пример2: { n }=1,2,3…. Это множество не имеет предельных точек. Определение предела функции по Коши. Пусть f(x) определена на Х и пусть a -предельная точка X. Число b называется пределом f (x) в точке a, если " e > 0 $ d > 0 такое, что " ч Î Ч б 0 Б / ч - ф / Б d Ж / а (ч) - и / Б e ю Число b называется пределом функции f (x) в точке a (при x ® a) если " e > 0 $ d > 0, такое, что " x Î X, 0 < | x - a | < d: | f (x) - b | < e. Обозначение: Множесво {0 < | x - a | < d} называется проколотой d-окрестностью точки a. Геометрическая интерпретация определения предела функции. (вставить рисунок) заметим, что 0 < | x - a | < d Û | f (x) - b | < e Û b - e < f (x) < b + e. С геометрической точки зрения тот факт, что y = b - e и y = b + e. При этом в самой точке a f (x) может быть не определена, либо её значение в данной точке может выходить за пределы данной полосы.
Замечание 1. Функция может иметь в данной точке только один предел. В самом деле, допустим, что f (x) имеет в точке a два предельных значения: b и c. Возьмём e столь малым, чтобы e-окрестности точек b и c не пересекались. Тогда для значений аргумента из проколотой окрестности точки a значения функции должны лежать одновременно в e-окрестности b и в e-окрестности точки c, чего не может быть так как эти e-окрестности не пересекаются. Функция y = f (x) называется ограниченной сверху (снизу) на множестве X, если $ число M (m), " x Î X: f (x) £ M (f (x) ³ m). При этом число M (m) называют верхней (нижней) гранью функции f (x) на множестве X. f (x) называется ограниченной на множестве X, если она ограничена на этом множестве и сверху и снизу, то есть $ M и m, " x Î X: m £ f (x) £ M. f (x) называется ограниченной на X,если $ A >0, " x Î X: | f (x) | £ A. Замечание 2. Если функция f(x) имеет предел в точке a, то она ограничена в некоторой окрестности этой точки. Утверждение следует непосредственно из определения предела.
Примеры: 1) f (x) = b = const (" x).
В самом деле, " e > 0 возьмем " d > 0. Тогда " x, | x - a | < d: | f (x) - b | = | b - b | = 0 < e. 2) f(x) = (рисунок)
3) f (x) = рисунок
4) f (x) = x (" x).
В самом деле, "e > 0 возьмём d = e. Тогда " x, | x - a | < d = e: | Это и означает, по определению предела, что 7) f (x) = sin (Pисунок) Предположим, что $ $ d > 0: " x, 0 < | x | < d: | sin Возьмём 0 < | sin При любом b подчёркнутые неравенства противоречат друг другу, и это доказывает, что
6) Докажем, что Предварительно докажем неравенствa sin x < x < tg x при 0 < x < (рисунок)
при 0 < | x | < возьмём d = e. Тогда. Если 0 < | x - 0 | < d = e, то | sin x - 0 | = | sin x | < | x | < e. Это и означает по определению, что
|

 {
{ 
 }
}
 f (x) = b.
f (x) = b.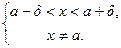



 - a | = | x - a | < e.
- a | = | x - a | < e.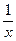 (x ¹ 0). Докажем, что
(x ¹ 0). Докажем, что  не существует.
не существует. = b. Возьмём e = 1. Согласно определению предела функции,
= b. Возьмём e = 1. Согласно определению предела функции, =
=  ,
,  =
=  . Тогда для достаточно большого натурального n будут выполнены неравенства:
. Тогда для достаточно большого натурального n будут выполнены неравенства: - b | < 1, т.е. | 1 - b | < 1, и также
- b | < 1, т.е. | 1 - b | < 1, и также - b | < 1, т.е. | 1 + b | < 1.
- b | < 1, т.е. | 1 + b | < 1.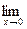 sin x =0.
sin x =0. .
. , то есть
, то есть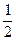 sin x <
sin x < 


