Теорема о пределе монотонной ограниченной функции.
f (x) называется 1) возрастающей на X, 2) убывающей на X, 3) невозрастающей на X, 4) неубывающей на X, если " 1) f ( 2) f ( 3) f ( 4) f ( Функции 1) - 4) называются монотонными на X, функции 1) - 2) называются строго монотонными на X. Примеры: 1) f (x) = 2) f (x) =[x]- неубывающая на (-¥, ¥). Пусть f (x)- ограниченна сверху на X, то есть $ M >0, " x Î X: f (x) £ M. Число М называется верхней гранью функции f (x) на множестве Х. Наименьшая из верхних граней ограниченной сверху на X f (x) называется её точной верхней гранью и обозначается Эквивалентное определение: Число M называется точной верхней гранью f (x) на X, если: 1) " x Î X: f (x) £ M. 2) " [7] Сформулировать аналогичное определение точной нижней грани функции. Пример: 1) 2) Различие случаев 1) и 2) в том, что в случае 1) функция принимает значения, равные Sup и Inf, а во втором не принимает. Теорема 2.7 Пусть f (x)- монотонная и ограниченная на полупрямой (а, + ¥), тогда существует Доказательство: Пусть, для определённости f (x) не убывает и ограничена сверху на (а, + ¥). Тогда она имеет на (а, + ¥) точную верхнюю грань. Введём обозначение: Зададим произвольное e > 0 и рассмотрим число b - e < b, по определнию точной верхней грани $ А: f (A) > b - e. Так как f (x) ³ f(a) при x ³ A, то f (x) > b - e при x ³ A, или b - f (x) < e при x ³ A, то есть | f (x) - b | < e при x ³ A. а это и означает, что Теорема доказана. Следствие: Монотонная ограниченная последовательность сходится. Замечание: Теорема, аналогичная теореме 7, имеет место для односторонних пределов функции, например: если f (x)- монотонная и ограниченная в некоторой правой полуокрестности точки а, то существует Рассмотрим последовательность: Докажем, что она монотонная и ограниченная. Нам понадобится неравенство Бернулли: Используя неравенство Бернулли, получаем:
= Следовательно, { Рассмотрим { Составим отношение Используя три неравенства: " n: 2 = Следовательно, последовательности { буквой е: lim
|

 и
и  Î X,
Î X, 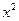 - возрастающая на [0, + ¥].
- возрастающая на [0, + ¥]. f (x).
f (x). < M $
< M $  Î X: f (
Î X: f ( f (x).
f (x). sin x = 1,
sin x = 1, 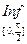 sin x = 0.
sin x = 0. sin x = 1,
sin x = 1,  sin x = 0.
sin x = 0. f (x).
f (x). f (x) = b. Докажем, что
f (x) = b. Докажем, что 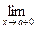 f (x). Пример
f (x). Пример =
=  .
. ³ 1 + nx "натурального n и " x > -1, причём при n > 1 знак равенства имеет место только для x = 0 (доказать самостоятельно по индукции).
³ 1 + nx "натурального n и " x > -1, причём при n > 1 знак равенства имеет место только для x = 0 (доказать самостоятельно по индукции). =
=  =
=  ×
×  =
=  ×
×  =
= ×
×  ×
×  >
>  }:
}:  =
=  . Отметим, что
. Отметим, что  , применим неравенство Бернулли и получим (аналогично тому, как было получено для последовательности {
, применим неравенство Бернулли и получим (аналогично тому, как было получено для последовательности {  >
>  , приходим к цепочке неравенств:
, приходим к цепочке неравенств: <
<  < … <
< … <  = 4.
= 4.



