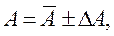ВЫЧИСЛЕНИЕ ПОГРЕШНОСТЕЙ ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ
В большинстве экспериментов интересующая нас величина непосредственно не измеряется. Вместо этого измеряются другие величины (аргументы)
Если для каждого аргумента в выражении (11) экспериментально найдены средние значения
получающееся при подстановке в выражение (11) вместо истинных значений аргументов их средних экспериментальных значений. Доверительная погрешность Полное приращение
где Рассматривая в выражении (12) величины
Таким образом, для того чтобы определить абсолютную погрешность результата косвенного измерения, следует найти частные производные функции При расчете погрешностей по формуле (13) допустимо пренебрегать теми слагаемыми подкоренного выражения, которые по крайней мере в 2 – 3 раза меньше максимального. (коэффициент 3 применяется в тех случаях, когда слагаемых много и малые погрешности могут внести заметный вклад в общую погрешность). Это соображение существенно упрощает расчет погрешности, а также позволяет четко выявить тот аргумент, погрешность которого имеет определяющее значение. Данный подход удобен при обсуждении результатов и важен для поиска путей повышения точности результатов. Если искомая функция
и вместо выражения (13) получают следующее соотношение
Заметим, что правая часть выражения (15) дает значение относительной погрешности Окончательно рекомендуется следующий алгоритм обработки результатов косвенных измерений. 1. Выполнить (однократные или многократные) прямые измерения аргументов
(Подразумевается, что величина 2. Найти среднеарифметические значение аргументов
3. Вычислить абсолютные погрешности отдельных результатов наблюдений для каждого аргумента (при многократных его измерениях), а также их квадраты и соответствующие суммы
4. Для данных значений
5. Если функция
В противном случае опредлить доверительную погрешность
6. Вычислить предварительный результат измерений
7. Округлив результат измерений и погрешность, записать окончательный результат в виде
|

 и т.д., а затем искомая величина
и т.д., а затем искомая величина  вычисляется на основе заданной функциональной зависимости
вычисляется на основе заданной функциональной зависимости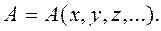 (11)
(11)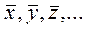 и вычислены погрешности
и вычислены погрешности 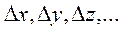 , то за наилучшее приближение для величины
, то за наилучшее приближение для величины  принимается значение
принимается значение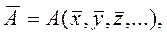
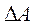 косвенных измерений величины
косвенных измерений величины 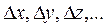 прямых измерений (однократных или многократных) всех аргументов
прямых измерений (однократных или многократных) всех аргументов 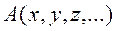 , обусловленное изменением ее аргументов
, обусловленное изменением ее аргументов 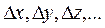 , может быть, как известно из курса высшей математики, c достаточной точностью вычислено по формуле
, может быть, как известно из курса высшей математики, c достаточной точностью вычислено по формуле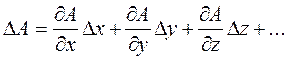 , (12)
, (12) ,
,  ,
, 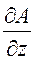 – частные производные функции
– частные производные функции 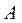 по ее соответствующим аргументам. При вычислении частной производной все аргументы функции
по ее соответствующим аргументам. При вычислении частной производной все аргументы функции  кроме того, по которому производится дифференцирование, считаются постоянными.
кроме того, по которому производится дифференцирование, считаются постоянными. . (13)
. (13)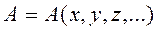 удобна для логарифмирования (представляет собой произведение простых функций измеряемых аргументов), учитывают, что полное приращение функции
удобна для логарифмирования (представляет собой произведение простых функций измеряемых аргументов), учитывают, что полное приращение функции  может быть с достаточной точностью рассчитано по формуле
может быть с достаточной точностью рассчитано по формуле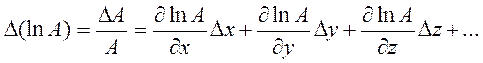 , (14)
, (14)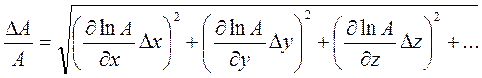 . (15)
. (15) результата данного косвенного измерения.
результата данного косвенного измерения.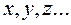 измеряемой функции
измеряемой функции 
 ;
; 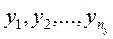 ;
; 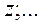 .
.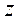 является результатом однократного прямого измерения.)
является результатом однократного прямого измерения.)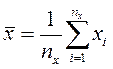 ;
; 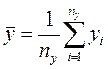 ;
; 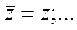 .
.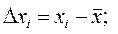
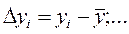
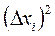 ;
; 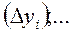
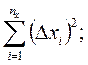

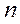 и
и 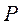 найти по таблице коэффициент Стьюдента
найти по таблице коэффициент Стьюдента 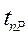 и вычислить погрешности аргументов (случайные или приборные)
и вычислить погрешности аргументов (случайные или приборные) .
. 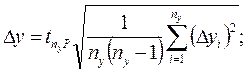 .
. 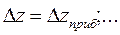 .
.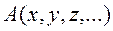 удобна для логарифмирования, прологарифмировать ее и по формуле (15) вычислить относительную погрешность
удобна для логарифмирования, прологарифмировать ее и по формуле (15) вычислить относительную погрешность .
. результата измерений по общей формуле (13)
результата измерений по общей формуле (13) .
. .
.