НЕВОСПРОИЗВОДИМЫЕ КОСВЕННЫЕ ИЗМЕРЕНИЯИногда при выполнении косвенных измерений невозможно повторить наблюдения в тождественных условиях относительно одного или нескольких аргументов измеряемой функции. Например, при измерении коэффициента вязкости жидкости в нее бросают металлические шарики (дробинки). Каждый из брошенных в жидкость шариков сразу же достать нельзя. Условия опытов, повторенных с разными шариками, не будут одинаковыми из-за различия размеров и формы шариков, различного состояния их поверхностей и т.д. В этом случае говорят, что косвенные измерения невоспроизводимы. Тем не менее коэффициент вязкости характеризует одну и ту же исследуемую жидкость, и расчет должен давать близкие значения этого коэффициента для всех шариков. Для невоспроизводимых косвенных измерений рекомендуется следующий порядок обработки их результатов. 1) Определить значение искомой функции
2) Каждое из определенных таким образом значений
а погрешность вычисляется по формуле (как случайная погрешность)
т.е. по правилам обработки результатов прямых многократных измерений.
|
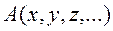для каждого 
ого невоспроизводимого наблюдения, исходя из найденных экспериментальных значений аргументов 
,
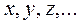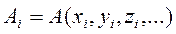
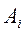рассматривается затем как случайная величина с нормальным законом распределения погрешностей 
. Иначе говоря, значения 
. В соответствии с этим в качестве наиболее вероятного значения берется среднее арифметическое
,
,
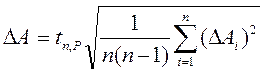