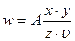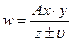Повышение точности и вычисление вероятной ошибки при многократных измерениях

 

Выше уже говорилось о том, что при проведении многократных изме­рений заданной величины при одних и тех же параметрах случайные ошибки проявляются в разбросе получаемых данных.

Если проведено несколько измерений искомой величины, то вполне
естественно, что наиболее достоверным результатом является средне­-
арифметическая величина из всех измерений. Используя в качестве
окончательного результата это среднеарифметическое значение, можно
в значительной мере снизить влияние случайных ошибок при измерениях.
Естественно, что чем больше произведено измерений, тем с большей
уверенностью исключаются случайные ошибки, и в пределе при бесконечно
большом числе измерений окончательный результат будет содержать
лишь систематическую ошибку.

Абсолютная случайная ошибка при нескольких измерениях величины
вычисляется по формуле

 

.

(65)

 

 

В этой формуле n – число измерений, w_cp – среднеарифмети­ческое значение из всех полученных величин w:

 

wcp=Σw/n.

(66)

 

Ошибка, вычисляемая по (65), называется квадратичной. Из самого вида (52) ясно, что при n → ∞; ошибка Δw_кв → 0.

Однако функция (52) такова, что увеличение количества измере­ний с 2 до 5 сильно снижает эту ошибку; с 5 до 10 – несколько меньше, а увеличение количества измерений, например с 20 до 30, уже очень мало меняет величину этой ошибки.

Заметим, что для вычисления рассматриваемой ошибки необходимо иметь полученные в результате эксперимента величины w, что не всегда требовалось для оценки ошибки отдельного измерения.

 

Таблица 7.1

 

Обозначения	Расчетная формула искомой величины	Формула для определения максимально возможной относительной ошибки
а	w = A · x · y · z	δw = δx + δy + δz
б	w = A · xα · yβ · zγ	δw = αδx + βδy + γ δz
в		δw = αδx + βδy + γ δz + lδυ
г		δw = δx + δy + δz + δυ
д	w = x ± y ± z
е	w = Ax ± By ± C z
ж
з
и	w = A ± Bx
к	w = A lnx
л	w = A eαx	δw = α x δx

 

Библиографический список

 

1. Теплотехника: Учебник для вузов / В.Н. Луканин, М.Г. Шатров и др.; Под ред. В.Н. Луканина. – М.: Высш. шк., 1999 – 671 с.

2. Кудинов В.А., Карташев Э.М. Техническая термодинамика: Учеб. пособие для вузов – М.: Высш. шк., 2000 – 261 с.

3. Стародубцев В.А. Техническая термодинамика: Учеб. пособие: Омск, ОмГТУ, 1999 – 126 с.

4. Рабинович О.М. Сборник задач по технической термодинамике. М., Машиностроение, 1973 – 344 с.

5. Техническая термодинамика: Учеб. для вузов / В.А. Кириллин, В.В. Сычев, А.Е. Шейдлин. 4–е изд. перераб. – М.: Энергоатомиздат, 1983–416 с.

6. Техническая термодинамика: Учеб. для машиностроит. спец. вузов / В.И. Крутов, С.И. Исаев и др.; Под ред. В.И. Крутова – 3–е изд. перераб. и доп. – М.: Высш. шк., 1991 – 384 с.
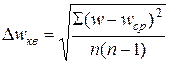