Условие равновесия частицы газа в межвенцевом зазоре
Рассмотрим упрощенное условие равновесия частицы газа с гранями dz, dr, rdθ; в межвенцевом зазоре (рис. 7.20) [6]. На частицу газа действуют центробежные силы, которые уравновешиваются силами давления. На нижнюю грань действует давление Р, на верхнюю Р+dР. Тогда сила давления: Условие равновесия
Поскольку правая часть выражения (7.23) даже при отрицательной закрутке всегда положительна (
Рис. 7.20. Равновесие частицы газа в межвенцевом зазоре
Массовый расход через элементарную ступень на некотором радиусе r:
Таким образом, наличие центробежных сил приводит к росту давления от втулки к периферии ( Попытка расчета пространственного потока на основе уравнений гидрогазодинамики сопряжена со значительными трудностями, а результат зачастую не имеет практического значения. Поэтому при проектировании ступеней осевого компрессора часто прибегают к следующим допущениям: 1) пренебрегают внешним теплообменом; 2) потери считают равными нулю или наперед заданными; 3) поток считается осесимметричным, т.е. параметры не изменяются в заданном сечении по углу разворота θ (оси u); 4) не рассматривают особенности течения внутри лопаточных аппаратов, а определяют параметры в межвенцевом зазоре; 5) не учитывают влияние пограничного слоя; 6) радиальную компоненту Сr считают пренебрежимо малой. Таким образом, задача сводится к определению зависимостей Воспользуемся уравнением Бернулли:
т.к.
Примем, что
т.к.
Возьмем из формулы (7.23)
Дифференциальное уравнение (7.26) имеет множество решений
где А 1, А 2, В 1, В 2 – коэффициенты, выбираемые так, чтобы они соответствовали дополнительным условиям изменения по радиусу одной из производных величин Наибольшее распространение получили такие законы закрутки, как: 1) закон постоянства циркуляции - 2) закон постоянства степени реактивности -
|

 .
. ,
, . (7.23)
. (7.23) ), то градиент давления
), то градиент давления  .
.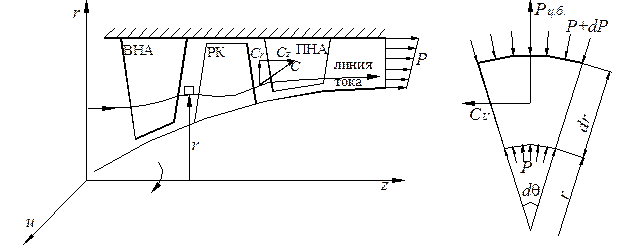
 .
. , т.е. поток имеет сложную пространственную структуру.
, т.е. поток имеет сложную пространственную структуру. и
и 
 , разделив на ρ;, получим
, разделив на ρ;, получим ,
, , то
, то  .
. и
и  по высоте лопатки r, тогда
по высоте лопатки r, тогда
 , (7.24)
, (7.24) то пренебрегая радиальным течением (Сr = 0):
то пренебрегая радиальным течением (Сr = 0):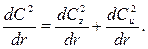 (7.25)
(7.25) и подставим его в (7.24) с учетом (7.25):
и подставим его в (7.24) с учетом (7.25): . (7.26)
. (7.26) и
и  Поэтому необходимо введение замыкающего соотношения. В теории турбокомпрессоров его называют законом закрутки и представляют в виде
Поэтому необходимо введение замыкающего соотношения. В теории турбокомпрессоров его называют законом закрутки и представляют в виде ,
, ,
, или
или 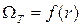 .
. ;
; 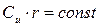 ;
; .
.


