Коэффициент уменьшения теоретического напора
Важным параметром, определяющим напорность ступени, является угол выхода потока из решетки РК в относительном движении β;2. Ранее были получены формулы для РК с бесконечным числом лопаток
и конечным числом лопаток
В РК с конечным числом лопаток поток отстает по направлению от угла лопаток на выходе (рис. 7.5) на величину Δβ=βл2–β2. Определение β;2 достаточно сложная задача, т.к. угол отставания потока Δ β; (5-15º)зависит от густоты решетки, аэродинамической нагруженности лопатки и состояния пограничного слоя на ней.
Наиболее простой способ определения β;2 по углу βл 2, по числу лопаток z 2 в предположении о существовании осевого вихря был предложен Аурелем Стодолой в 1929 году. Из выходных треугольников скоростей (рис. 7.6) следует, что конечное число лопаток приводит к уменьшению теоретического напора (hT < hT ∞), т.к. Сu 2< Сu 2∞, которое оценивается коэффициентом уменьшения теоретического напора m.
Если Cu 1=0, тогда Из треугольника скоростей При бесконечном числе лопаток
Рис. 7.6. Выходные треугольники скоростей при конечном числе лопаток (сплошные линии) и z =∞ Согласно гипотезе о существовании осевого вихря следует, что направление его вращения противоположно вращению рабочего колеса, а угловые скорости одинаковы wо.в.= w. Кроме того, окружной составляющей осевого вихря является разность проекций относительной скорости
Обозначив а – диаметр вписанной в межлопаточный канал окружности (диаметр осевого вихря), найдем
можно считать что
т.к.
Далее можно определить угол выхода потока β2 и коэффициент μ. Определим угол β2:
Из соотношений треугольника скоростей, учитывая что Wr2 = Сr2 и φ;2 =Сr 2 /U 2:
Подставив (7.11) в (7.1) получим формулу А. Стодолы для расчета коэффициента теоретического напора. Определим коэффициент уменьшения теоретического напора. Для этого из треугольника скоростей выразим Сu 2∞:
сократим последнее на U 2
или учитывая формулу (7.1)
Формулы (7.12) и (7.13) называются формулами Стодолы и справедливы для РК с лопатками, выполненными по дуге окружности и βл 2<90º. Кроме формулы А. Стодолы есть и другие формулы для определения m, которые носят частный характер. Для закрытых рабочих колес, меридиональное сечение которых спрофилировано по закону b × R =const применяются формулы Б. Экка, учитывающие влияние кривизны межлопаточного канала [6]
формула (7.15) учитывает, кроме того, уменьшение на 20–30 % сечения потока на выходе из межлопаточного канала из-за наличия срывной области. Для полуоткрытых рабочих колес с bл 2 = 90° можно использовать формулу П.К. Казанджана
где К. Пфляйдерером предложена следующая формула [3, 13]
где а – опытный коэффициент (обычно а =1,2). Погрешность в определении теоретического напора по приведенным формулам может достигать 20–30 %, так как формулы носят эмпирический характер. Надежно определить m с погрешностью 2–3 % - можно с помощью метода теории решеток [6].
7.1.3. Влияние сжимаемости (чисел Маха) на характер потока
Число Маха представляет собой отношение скорости газового потока к скорости звука в данном сечении
При больших скоростях, когда числа Маха достаточно велики (обычно > 0,5), проявляется такое свойство газа, как сжимаемость, т.е. увеличение плотности движущегося потока по сравнению с неподвижным. Рассмотрим это на примере. Определим сжимаемость
Из уравнений изоэнтропийного течения
Подставим теперь в формулу (7.18) значения k и R для воздуха и водорода: - для воздуха
- для водорода
Из полученного результата следует, что при движении с одинаковыми скоростями сжимаемость воздуха проявляется сильнее, чем водорода.
Течение газа в решетках осевых и центробежных компрессоров носит диффузорный характер, поэтому максимальные значения скоростей достигаются на входе в решетки РК (W 1) и ПНА или диффузора (С 3). Соответственно и числа Маха, рассчитанные по этим скоростям, будут иметь определяющие значения (МW 1 и МС 3). По значениям чисел Маха ступени компрессоров делятся: 1) на дозвуковые (М <1); 2) сверхзвуковые (М >1); 3) трансзвуковые (М ><1 по высоте или длине лопатки). При значениях МW 1 меньше, но близких к 1, поток газа, сужаясь от входа в решетку до ее «горла» становится сверхзвуковым (рис. 7.7). В этом случае возможно возникновение скачка уплотнения, приводящего к росту потерь в решетке. Значения чисел Маха МW 1, при которых в самом узком проходном сечении решетки возникает скорость, равная местной скорости звука – называются критическими (Мкр). C ростом МW 1 начало возникновения отрыва пограничного слоя (момент резкого увеличения коэффициента лобового сопротивления Сw) резко сдвигается влево (рис. 7.8а), в область меньших углов атаки i. Увеличение изогнутости профиля fмах / В снижает величину Мкр (рис. 7.8б). Таким образом, рост чисел Маха, то есть рост W 1 и С 3 приводит к увеличению потерь в решетке, особенно на нерасчетных режимах (
Рис. 7.8. Зависимости аэродинамических коэффициентов от числа Маха на входе в решетку РК, углов атаки и изогнутости профиля
Рис. 7.9. Профили лопаток осевых ступеней: а) дозвуковых; б) сверхзвуковых При сверхзвуковом обтекании решетки из профилей с тупой передней кромкой, образуются прямые скачки уплотнения, в этом случае значительно возрастают волновые потери. Для уменьшения потерь желательно иметь косые скачки уплотнения, что возможно при заостренных входных кромках. Решетка профилей проектируется таким образом, чтобы в межлопаточных каналах возникало два скачка уплотнения: косой и прямой. Суммарные потери в двух скачках будут меньше потерь при одном прямом скачке. Максимальным числом Маха (Мmax) называют величину МW 1 или МС 3, при которой в самом узком («горловом») сечении канала между лопатками возникает скорость, равная скорости звука, т.е. достигается максимально возможный расход через решетку. Дальнейшее увеличение расхода через решетку невозможно, т.к. происходит «запирание» решетки.
|

 (7.8)
(7.8) .
.
 . (7.9)
. (7.9) .
. .
. ;
;  ; β2 = βл 2.
; β2 = βл 2.
 .
. ,
, , тогда
, тогда ,
, , то
, то . (7.10)
. (7.10) .
. . (7.11)
. (7.11) ,
, ,
, , (7.12)
, (7.12) . (7.13)
. (7.13) , (7.14)
, (7.14) , (7.15)
, (7.15) , (7.16)
, (7.16) – средний диаметр входного сечения колеса.
– средний диаметр входного сечения колеса. , (7.17)
, (7.17) .
. при скорости С =250 м/с для воздуха (k =1,4; R =287 Дж/(кг·К)) и водорода (k =1,4; R =4206 Дж/(кг·К)). Выведем расчетную формулу
при скорости С =250 м/с для воздуха (k =1,4; R =287 Дж/(кг·К)) и водорода (k =1,4; R =4206 Дж/(кг·К)). Выведем расчетную формулу ,
,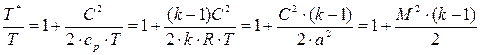 .
. ,
, ,
, . (7.18)
. (7.18) ,
, ;
; ,
, .
. ). В связи с этим профилирование лопаток в сверхзвуковых ступенях осевых компрессоров значительно отличается по форме от лопаток дозвуковых ступеней (рис. 7.9).
). В связи с этим профилирование лопаток в сверхзвуковых ступенях осевых компрессоров значительно отличается по форме от лопаток дозвуковых ступеней (рис. 7.9).
 а) б)
а) б) а) б)
а) б)


