Кинематические схемы рабочих колес центробежных компрессоров с различной степенью реактивности
Определим, при какой степени реактивности будет максимальное повышение давления в ступени центробежного компрессора. В известном уравнении
примем, что
разделив левую и правую части на
Выразим ψд через ψТ
После чего получим
Из уравнения (5.26)
Из анализа зависимостей следует, что: - при - при Для того, чтобы найти экстремум, нужно взять производную от ψп по ψТ и приравнять ее к нулю
из чего видно, что при Таким образом, в случае Ранее, в гл. 5, было показано, что коэффициент теоретического напора, степень реактивности и другие безразмерные параметры зависят от угла потока в относительном движении на выходе из колеса и коэффициента расхода. Изобразим эти зависимости графически (рис. 6.1) для рабочего колеса с бесконечным числом лопаток (zл → ∞), имеющего коэффициент расхода Из рис. 6.1 виден диапазон углов 11,3º<β2<168,1º (для заданного коэффициента расхода φ;2=0,2) в котором происходит повышение давления в колесе. Чем выше коэффициент расхода, тем этот диапазон становится уже. Рассмотрим три схемы рабочих колес центробежного компрессора при одинаковых скоростях U 2 и Cr 2, но имеющих различные степени реактивности Ω Т = 1,0; 0,5; 0. Эти схемы показаны на рис. 6.2.
а) Рис. 6.2. Кинематические схемы колес: а) с лопатками загнутыми назад; б) с лопатками радиальными на выходе; в) с лопатками загнутыми вперед
Далее построим зависимости коэффициента теоретического напора и кинематической степени реактивности от коэффициента расхода при различных значениях угла лопаток на выходе βл 2, используя для этого формулы (5.9) и (5.26). Зависимости эти, приведенные на рис. 6.3, будем называть теоретическими характеристиками. Из этих графиков виден принципиально различный характер изменения подводимой к газу работы, при изменении расхода, в рабочих колесах, имеющих углы выхода βл 2<90°, βл 2>90° и βл 2=90°.
Рис. 6.3. Теоретические характеристики для рабочих колес с загнутыми
Из рис. 6.1, 6.2 и 6.3 можно сделать следующие выводы: 1. Максимальный коэффициент напора создают РК с лопатками загнутыми вперед βл 2>90º. Однако они имеют самую большую скорость на выходе С 2 из представленных ступеней, что приводит к росту потерь в диффузоре и снижению КПД ступени в целом. Поэтому такие РК находят применение только в низконапорных вентиляторах. 2. РК реактивного действия с загнутыми назад лопатками (βл 2<90º) обладают высоким КПД и применяются в основном в стационарных компрессорах. Различают РК насосного (βл 2=15-30º) и компрессорного (βл 2=30-60º) типа. 3. РК с лопатками, имеющими радиальный выход (βл 2=90º), создают высокий напор, но КПД ступени несколько ниже, чем при загнутых назад лопатках. РК с βл 2=90º полуоткрытого типа имеют одно основное преимущество: окружные скорости U 2, ограниченные пределом прочности примерно в 1,5 раза выше, чем у РК с покрывающим диском, что обеспечивает большие степени повышения давления в одной ступени. Такие РК применяются в авиационных компрессорах и компрессорах наддува двигателей внутреннего сгорания.
6.2. Кинематические схемы рабочих колес осевых компрессоров с
Пропускную способность ступеней осевых компрессоров характеризует коэффициент расхода
Характерная окружная скорость – скорость на концах лопаток Из соотношений треугольников скоростей осевой ступени:
Из (6.4) следует, что если углы α; и β; возрастают, то возрастает и расходная скорость Cz. Напорность ступени определяется коэффициентом теоретического напора, который в ступенях осевых компрессоров имеет значение близкое к значению коэффициента внутреннего напора из-за пренебрежительной малости на трение дисков и протечки по сравнению с центробежными компрессорами
Ранее, в разд. 5, было получено выражение, определяющее влияние геометрии ступени на ψТ при условии
На самом деле, даже в пределах одной ступени, разница между диаметрами сечений на входе и выходе может быть заметной (рис. 6.4).
Определим теперь влияние геометрии ступени на ψТ и hТ при
подставим его в уравнение Эйлера
Учитывая соотношения
разделив на
Таким образом, формула (6.2) является частным случаем формулы (6.6). Из формулы (6.6) видно, что ψТ тем больше, чем больше разворот потока в ступени
здесь ψТ – коэффициент напора элементарной ступени на некотором радиусе r 1. Другим важным параметром, определяющим эффективность работы ступени, является степень реактивности
Найдем связь Ω Т с ψТ. По определению коэффициент напора
Из формулы (6.8) следует
где
Построим треугольники скоростей (рис. 6.5) для Ω Т = 0; 0,5; 1 и при различных закрутках потока на входе По горизонтали расположены треугольники скоростей для ступеней с постоянным значением Ω Т, по диагонали – с постоянной закруткой на входе, в результате, по вертикали расположены треугольники скоростей для ступеней с ψТ =const. Наглядно видно, что рост ψТ при Таким образом, при больших значениях угла поворота потока ε; и высоких значениях W 1 и С 2 достигаются высокие значения коэффициентов теоретического напора. Однако на практике значения его ограничены пределом ψТ = 0,35 – 0,4 в основном из-за двух факторов: 1) роста чисел Маха на входе в РК и НА (МW 1 и МС 2), приводящего к резкому увеличению профильных потерь. 2) роста диффузорности решеток и связанных с этим потерь (отрыв пограничного слоя) и явлений потери устойчивости (вращающийся срыв).
Перечисленные факторы следует рассматривать в рамках двухмерной теории течения газа в решетках компрессорных машин динамического действия с учетом сжимаемости и вязкости газа. В последующих разделах эти явления будут рассмотрены.
7. Особенности пространственного потока в ступенях компрессорных
Одномерная теория, при которой параметры потока считаются одинаковыми в каждой точке контрольного сечения, весьма эффективна при прикидочных расчетах и обработке экспериментальных данных. Но с помощью нее невозможно решать такие важные задачи как профилирование ступени в радиальной и меридиональной плоскостях, а кроме того, некоторые явления, имеющие место в турбокомпрессорах, не укладываются в рамки одномерной теории. Поэтому на практике при проектировании ступеней широко применяют двухмерные и квазитрехмерные модели. Говоря о двухмерной модели, будем предполагать, что течение происходит в параллельных плоскостях и что в каждой из них распределение давлений и скоростей одинаково. Основные задачи теории турбокомпрессоров сводятся к изучению обтекания решеток профилей заданной формы – прямая задача и к построению решеток для заданного отклонения потока – обратная задача.
|


 , тогда
, тогда ,
, , перейдем к безразмерным параметрам
, перейдем к безразмерным параметрам .
. . (6.1)
. (6.1) . (6.2)
. (6.2) . (6.3)
. (6.3)

 и
и  ,
,

 и
и  ,
, ,
,
 и
и  .
.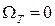 вся подводимая к газу энергия идет на увеличение динамического напора, а давление внутри рабочего колеса не повышается. В случае
вся подводимая к газу энергия идет на увеличение динамического напора, а давление внутри рабочего колеса не повышается. В случае 





 в)
в) 
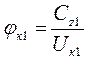 ;
;  .
. находится обычно в пределах Uк =450-500 м/с (для сравнения в центробежных компрессорах U2 =250-350 м/с). Расходные скорости: на входе в первые ступени Сz 1=200-230 м/с; на выходе последних ступеней Сz 2=80-100 м/с. Соответственно диапазон изменения коэффициентов расхода в пределах проточной части компрессора достаточно широк φк =0,16-0,5.
находится обычно в пределах Uк =450-500 м/с (для сравнения в центробежных компрессорах U2 =250-350 м/с). Расходные скорости: на входе в первые ступени Сz 1=200-230 м/с; на выходе последних ступеней Сz 2=80-100 м/с. Соответственно диапазон изменения коэффициентов расхода в пределах проточной части компрессора достаточно широк φк =0,16-0,5. . (6.4)
. (6.4) .
. и
и  :
: . (6.5)
. (6.5) Рис. 6.4. Схема РК осевого компрессора в меридиональной плоскости
Рис. 6.4. Схема РК осевого компрессора в меридиональной плоскости
 и
и  . Из треугольника скоростей
. Из треугольника скоростей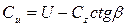 ,
,
 .
. →
→ 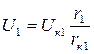 и
и  , обозначив
, обозначив  , запишем
, запишем ,
,
 ,
, . (6.6)
. (6.6) , чем больше торможение осевой скорости φк 2 < φк 1 и чем сильнее увеличение среднего радиуса r 2 > r 1. Основной вклад, безусловно, вносит угол разворота потока ε;, поэтому часто формулу (6.6) приводят в упрощенном виде:
, чем больше торможение осевой скорости φк 2 < φк 1 и чем сильнее увеличение среднего радиуса r 2 > r 1. Основной вклад, безусловно, вносит угол разворота потока ε;, поэтому часто формулу (6.6) приводят в упрощенном виде: , (6.7)
, (6.7) . (6.8)
. (6.8) .
. , (6.9)
, (6.9)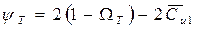 , (6.10)
, (6.10) .
. =-0,5;
=-0,5;  сопровождается снижением Ω Т, увеличением угла разворота потока ε; и возрастанием абсолютной скорости на выходе С 2 (числа Маха МС 2), а при Ω Т = const рост ψТ возможен при уменьшении положительной и увеличении отрицательной закрутки потока на входе, что также сопровождается возрастанием С 2 (МС 2), но кроме того, еще и W 1 (МW 1).
сопровождается снижением Ω Т, увеличением угла разворота потока ε; и возрастанием абсолютной скорости на выходе С 2 (числа Маха МС 2), а при Ω Т = const рост ψТ возможен при уменьшении положительной и увеличении отрицательной закрутки потока на входе, что также сопровождается возрастанием С 2 (МС 2), но кроме того, еще и W 1 (МW 1).



