Критическая частота вращения и условия виброустойчивости ротора
Еще на стадии проектирования проточной части турбокомпрессора возникает необходимость определения собственной частоты колебаний ротора. При совпадении ее с вынужденной частотой колебаний, т.е. с рабочей частотой вращения ротора, возникает явление резонанса, приводящее к резкому увеличению амплитуды колебаний ротора. Собственную частоту колебаний ротора называют критической и нормальная работа при ω;= ωкр невозможна. Рассмотрим условия резонанса неуравновешенного невесомого однодискового ротора (рис. 13.4). Примем ряд допущений: 1) диск расположен на равном расстоянии от опор (посередине пролета) для того, чтобы не учитывать влияние гироскопического момента на прогиб ротора; 2) ротор расположен вертикально для того, чтобы не учитывать влияние веса вала; 3) вся масса диска m сосредоточена в центре масс – точке С; 4) влияние момента инерции диска не учитывается; 5) опоры ротора считаются абсолютно жесткими. Небалансом ротора называется несовпадение центра масс с осью вала. Величина небаланса характеризуется эксцентриситетом е =О1С. При вращении ротора его небаланс приводит к возникновению центробежной силы, которая тем больше, чем больше число оборотов ротора:
Центробежная сила уравновешивается упругой силой вала, которая пропорциональна деформации, а коэффициент пропорциональности зависит от расстояния между опорами и от условия защемления в опорах:
где k – жесткость вала [Н/м] – сила, вызывающая прогиб вала равный 1 м (δ11 – коэффициент влияния [м/Н] – прогиб вала в точке крепления диска от силы равной 1 Н). Например, для вала постоянного сечения
где Е – модуль продольной упругости материала вала, Па; I – момент инерции поперечного сечения вала м4; L – длина вала. Из условия равновесия
Выразим прогиб вала
Проанализируем выражение (13.8). По мере увеличения ω; величина у возрастает. При достижении угловой скорости некоторого значения, при котором знаменатель выражения (13.8) становится равным нулю, величина прогиба достигает ∞. Это значение ω; является критическим:
Тогда (13.8) с учетом (13.9)
Проанализируем формулу (13.10). При ω;< ωкр. расстояние между точками О и С равно сумме При ω;= ωкр величина прогиба неограниченно возрастает. Этот случай соответствует резонансным колебаниям. В действительности прогиб имеет конечную величину из-за наличия сил трения дисков об окружающую среду и влияния жесткости опор.
При ω;> ωкр, когда При ω; → ∞ центр масс стремится занять положение на оси вращения, а величина прогиба становится равной эксцентриситету: у = - е. Происходит самоцентрирование ротора. Графический анализ формулы (13.10) показан на рис. 13.5 а [26]. Обычно криву Смещение центра масс (точки С) относительно оси вращения (точки О) происходит вследствие наличия прецессионного движения роторов. Поскольку вращающийся ротор прогибается на величину y, то он вращается с угловой скоростью ω; вокруг своей оси (точки О1), при этом прогнувшийся ротор может вращаться вокруг оси вращения (точки О) с угловой скоростью Ω (собственная частота колебаний). Если направления угловых скоростей ω; и Ω совпадают, то прецессионное движение называют прямым, если противоположны – то обратным. Если ω; = Ω, прецессионное движение называется синхронным. При этом условии возникает явление резонанса, т.е. это значение вынужденной частоты колебаний является критическим ωкр.
Рис. 13.5. Изменение прогиба ротора в зависимости
В большинстве случаев имеет место прямая прецессия, появляющаяся вследствие несбалансированности дисков, насаженных на вал. Обратная прецессия возникает, как правило, при идеально уравновешенных роторах. Рассмотренный пример определения критической частоты (рис. 13.4 формула (13.9)) приведен при многих упрощающих допущений. В действительности, на величину прогибов оказывают влияние следующие факторы: - количество дисков, насаженных на вал; - собственная масса вала и форма поперечного сечения вала; - смещение дисков относительно середины вала, следствием чего является гироскопический момент, препятствующий прогибам вала; - смещение центра масс диска, относительно точки его закрепления на валу (для консольных роторов); - влияние упругости опор ротора. Количество дисков, насаженных на вал определяет возможную форму колебаний ротора (рис. 13.6). При одном диске возможна лишь 1-я форма колебаний (рис. 13.6а), она близка к линии статического прогиба вала. В случае двухдискового ротора возможны как 1-я, так и 2-я формы колебаний (рис. 13.6б) в зависимости от того, как смещены друг относительно друга точки центра масс дисков. Теоретически возможны и более высшие формы колебаний (рис. 13.6в), однако в действительности происходит разбивка центров масс на группы, и практически встречаются либо 1-я, либо 2-я формы колебаний. 1-й форме колебаний соответствует одно условие резонанса, при 2-й форме существуют два условия резонанса: при первой ωкр I и второй ωкр II критических частотах вращения.
Рис. 13.6. Формы упругой линии вала при различных критических частотах:
Определение критических частот вращения многодискового ротора – трудоемкая задача. Расчетом возможно определить только первую критическую частоту вращения ротора ωкрI, поскольку 1-я форма колебаний близка к линии статического прогиба. На практике широко используются несколько приближенных методов определения первой критической частоты ωкрI: - метод Донкерли; - метод Рэлея; - метод приведения. Примеры расчетов по этим методам приведены в [47]. Рассмотрим теоретические предпосылки метода Рэлея, получившего наибольшее распространение вследствие его большей точности. Расчет первой критической частоты вращения по методу Рэллея Реальный многодисковый ротор прогибается под действием собственного веса и веса дисков, насаженных на него, на величину статического прогиба y 0 (рис. 13.7). При вращении ротора вал прогнется вследствие небаланса еще на дополнительную величину у и будет колебаться относительно линии статического прогиба вала. Однако это незначительно сказывается на критической частоте вращения.
Рис. 13.7. Расчетная схема определения критической частоты по методу Рэллея
Согласно методу Рэллея частота собственных колебаний определяется из условия, что полная энергия системы, совершающей свободные колебания, остается постоянной
где П – потенциальная энергия системы; К – кинетическая энергия системы. Максимальная потенциальная энергия изгиба вала с сосредоточенными нагрузками получается при максимальном отклонении от положения равновесия (
где Fi – силы, приложенные к валу от массы дисков, насаженных на него, Н; yi – прогиб вала под действием силы Fi. Максимальная кинетическая энергия ротора при колебаниях будет при прохождении положения равновесия (
Из условия
При определении собственной частоты колебаний системы по уравнению (13.11) необходимо знать форму упругой линии вала, т.е. значений уi по участкам ротора. Таким образом, при расчете первой критической частоты по методу Рэллея вычерчивают эскиз ротора, разбивают его на участки (с сосредоточенными нагрузками или без них), определяют моменты инерции и массовые характеристики участков, а далее рассчитывают форму линии статического прогиба и по формуле (13.11) определяют ωкрI. Вторая критическая частота может быть определена по соотношению:
Для выполнения условий виброустойчивости (безрезонансной работы) ротора значение рабочей (вынужденной) частоты вращения должно выбираться с некоторым запасом от первой и второй критических (собственных) частот. Поэтому условия виброустойчивости записываются в следующем виде: - для жестких роторов - для гибких роторов Однако даже при безрезонансной работе ротора он должен пройти тщательные статическую и динамическую балансировки.
|

 .
. ,
, ,
,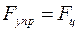
 .
. . (13.8)
. (13.8) ,
, . (13.9)
. (13.9) . (13.10)
. (13.10) . Поэтому при дальнейшем росте ω; центробежная сила Fц . также растет, как вследствие увеличения ω;, так и величины
. Поэтому при дальнейшем росте ω; центробежная сила Fц . также растет, как вследствие увеличения ω;, так и величины 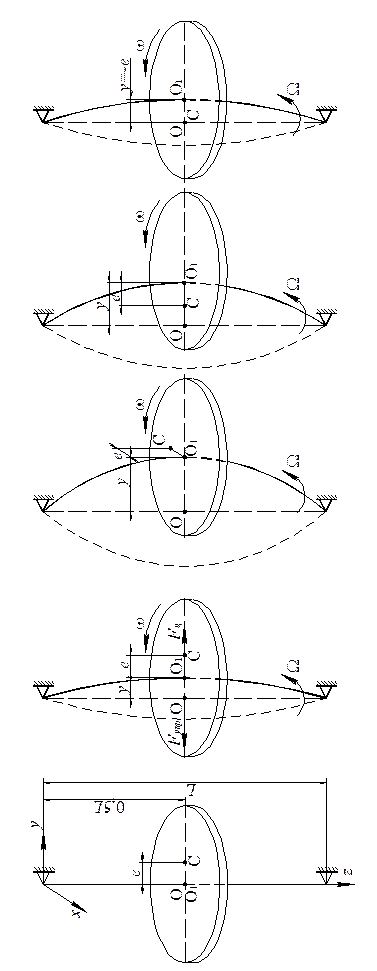
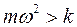 , знаменатель выражения (13.8) становится отрицательным и возрастает по абсолютной величине, следовательно прогиб у становится также отрицательным и уменьшается по абсолютной величине. Это возможно лишь при снижении центробежной силы, а т.к. угловая скорость растет, то расстояние между точками О и С (рис. 13.4г) равно по абсолютной величине разности
, знаменатель выражения (13.8) становится отрицательным и возрастает по абсолютной величине, следовательно прогиб у становится также отрицательным и уменьшается по абсолютной величине. Это возможно лишь при снижении центробежной силы, а т.к. угловая скорость растет, то расстояние между точками О и С (рис. 13.4г) равно по абсолютной величине разности  , и центр масс занимает положение по внутреннюю сторону от оси вала (т. С левее т. О1 на рис. 13.4 г). Такие роторы называют гибкими.
, и центр масс занимает положение по внутреннюю сторону от оси вала (т. С левее т. О1 на рис. 13.4 г). Такие роторы называют гибкими.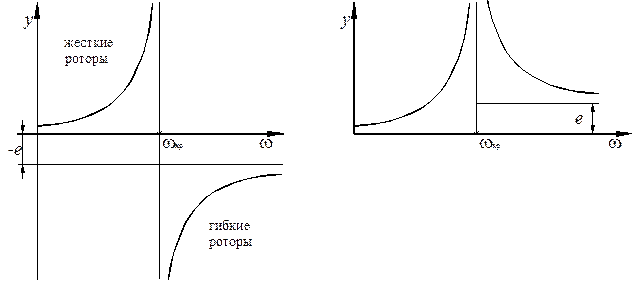 а) б)
а) б) а) б) в)
а) б) в)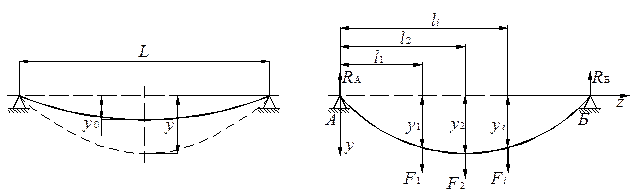
 ,
, ). В этом случае
). В этом случае  и
и ,
, ).В этом случае
).В этом случае 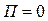 .
.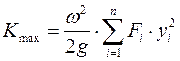 .
.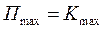 :
: . (13.11)
. (13.11) .
. ;
;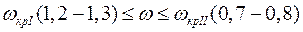 .
.


