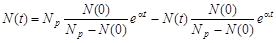Нелінійність математичних моделей

У низці випадків у науковій та навчальній літературі для спрощення обмежуються здебільшого лінійними моделями, хоча в наш час бурхливо розвивається науковий підхід — «синергетична економіка», — який спирається на суттєву нелінійність еконо-
мічних процесів, досліджує час і зміни в нелінійній економічній теорії[2].

У математичному аспекті важливим є поняття лінійності, котре означає, що справедливим є принцип суперпозиції, тобто, що будь-яка лінійна композиція розв’язків (наприклад сума їх) є також розв’язком задачі. Використовуючи принцип суперпозиції, неважко, відшукавши рішення в будь-якому частковому випадку, побудувати рішення для більш загальної ситуації. Тому про якісні властивості загального випадку можна судити виходячи з властивостей часткового — різниця між двома розв’язками має лише кількісний характер. Отже, у випадку лінійних моделей відгук (реакція) об’єкта на зміну умов є пропорційним величині цих змін.

Для нелінійних явищ, математичні моделі котрих не підпорядковуються принципу суперпозиції, знання стосовно до поведінки частини об’єкта ще не гарантують знань про поведінку об’єкта в цілому, а його відгук на зміну умов може якісно залежати від кількісної величини (обсягів) цих змін.

Наголосимо, що більшість реальних процесів і відповідних (адекватних) їм математичних моделей є нелінійними. Лінійні ж моделі відповідають досить частковим випадкам і, як правило, послуговують лише як перше наближення до реальності. Наприклад, моделі популяцій відразу ж стають нелінійними, якщо зважувати на те (взяти гіпотезу), що обмеженість доступних популяції ресурсів необхідно обов’язково враховувати. Будуючи такі моделі, вважають, що:

1) існує «рівноважна» чисельність популяції N_p, котру може забезпечити навколишнє середовище (з погляду сьогодення);

2) швидкість зміни чисельності популяції пропорційна цій чисельності, помноженій (на відміну від моделі Мальтуса) на величину відхилення її від рівноважного значення чисельності, тобто:

(2.2)

Співмножник у цьому рівнянні забезпечує механізм «насичення» чисельності — за N < N_p (N > N_p) швидкість зростання додатна (від’ємна) і прямує до нуля, якщо N ® N_p.

Подамо рівняння (2.2) у вигляді:

Інтегруючи це рівняння, отримаємо:

Постійну інтегрування C можна отримати з умови N (t = 0) =
= N (0), тобто

Отже, маємо:

або

Поведінка функції N (t) описується так званою логістичною кривою N (t) (рис. 2.2).

Рис. 2.2. Логістичні криві, що відповідають різним
значенням початкової чисельності N (0)

За будь-якого N (0) чисельність прямує до рівноважного значення N_p і, що характерно, тим повільніше, чим ближче N (t) до N (0). Отже, рівновага, на відміну від моделі (2.1), у даному випадку є стійкою. Зазначимо, що логістична модель більш реалістично відображає динаміку популяції порівняно з моделлю Мальтуса, але сама вона в разі необхідності стає нелінійною й тому більш складною. Наголосимо, що припущення щодо механізмів насичення використовуються у формуванні низки моделей різних економічних об’єктів і процесів як на мікро-, так і на макроекономічному рівнях.