Измерение количества информации
В теории информации сам этот термин применяется именно к измеримой,описываемой математически стороне сообщения [6, 7. 8]. Например, когда вы бросаете игральную кость, выпадает одно из шести равновероятных чисел. Вероятность выпадения каждого из них составляет: ρ = 1/6. Таким образом, при каждом броске игрок устраняет одно и то же количество неопределенности,т. е. у каждого броска одинаковое измеримое информационное содержание. Обобщая, можно сказать, что информация-это выраженное количественно уменьшение неопределенности в знаниях о событии. Следовательно, чем необычнее некоторое событие, т. е. чем меньше его вероятность р, тем больше уменьшается неопределенность, когда оно происходит. Поэтому информационное содержание (I) удобно выражать как величину, обратную этой вероятности: I = 1/р. Имеет смысл также условиться, что, когда событие точно произойдет (т.е. его вероятность p=1), его информационное содержание l = 0. Соответственно, измеримое информационное содержание I сообщения определяется следующим образом:
В этой формуле Id означает двоичный логарифм,т. е. логарифм по основанию 2 (Id — log2). 172 ЧАСТЬ II. ДВИГАТЕЛЬНЫЕ И ИНТЕГРАТИВНЫЕ ФУНКЦИИ НЕРВНОЙ СИСТЕМЫ
Вычислим теперь информационное содержание каждого броска игральной кости: I = Id 1/(1/6) = = Id 6 = 2,58 бит. Что такое «бит», мы рассмотрим ниже. Поскольку у карманных калькуляторов обычно нет программы для вычисления двоичного логарифма, можно использовать следующую формулу перевода:
Вообще говоря, вероятность появления каждого из множества η возможных символов (или состояний источника информации) составляет ρ = 1/n. Следовательно, уравнение (1) можно преобразовать к виду
Иными словами, информационное содержание I-это двоичный логарифм числа n всех символов или возможных состояний источника информации. Ниже мы применим такое соотношение к нейрофизиологии (с. 173 и далее). Символы с неодинаковой вероятностью появления. При выводе уравнения (2) упрощенно допускалось, что все n состояний источника информации равновероятны: ρ = l/n. Это верно, например, при бросании игральной кости. Однако обычно отдельные символы или состояния источника информации не равновероятны. Например, в текстах на английском языке буква «е» встречается чаще прочих, а буква «z»-сравнительно редко. Хотя такая неодинаковая вероятность сигналов наиболее распространенный случай, мы не будем его рассматривать для простоты изложения. В приведенном выше количественном определении информации никак не оговаривается ее значимость для пользователя. Например, при игре в кости разные выпадающие числа воспринимаются игроком отнюдь не одинаково: все зависит от характера игры, ее правил, предыдущего результата, результатов других игроков и т. п. Эти аспекты, называемые семантическими,теорией информации игнорируются. Двоичные и недвоичные символы; бит. В простейшем случае информацию можно передавать с помощью всего двух символов, в так называемой двоичной системе (например, нулями и единицами). При этом источник информации сигнализирует о выборе между двумя альтернативами (например, «да»/«нет»). Двоичные системы особенно удобны с точки зрения технической реализации (свет/темнота, включено/выключено, сильное/слабое магнитное поле и т.д.). В этом одна из причин выбора в качестве элементарной единицы информации информационного содержания двоичного символа: I = = Id 2 = 1. Количество информации, передаваемое одним двоичным символом, называется один бит. Бит-это очень мало информации. Если в такой системе требуется передать достаточно длинные сообщения, слова нужно составлять, объединяя по несколько символов. Длина слова (число в нем двоичных символов) непосредственно выражает количество информации в битах. Число слов, которые можно образовать из двух двоичных символов, равно 22 = 4: 00, 01, 10, 11. Из трех символов составляются 23 = 8 слов-комбинаций: 000, 001,
|

 (1)
(1)

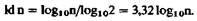
 (2)
(2)


