Передача координат с вершины знака на землю
Координаты пунктов полигонометрических и теодолитных ходов нередко вызывают необходимость вычислять в единой системе с пунктами опорных сетей высшего класса. Нередко при привязке к пунктам геодезической сети возникают случаи, когда начало или конец хода надо привязать к пункту уже построенной сети, недоступному для установки теодолита (шпиль здания, башни и т.д.). В этом случае решают задачу по перенесению координат с вершины знака на землю. Для решения этой задачи на расстоянии 50-100 м от недоступного пункта А геодезической сети выбирают точку Р с таким расчетом, чтобы с неё кроме пункта А было возможно измерить направления на пункты геодезической сети В и С (один из них необходим для контроля) и удобно было измерить два базиса b и b¢ для определения недоступного расстояния АР = d (рисунок 13). Для решения задачи с контролем помимо базисов b и b¢ измеряют шесть углов. Точность угловых и линейных измерений при этом должна быть не ниже точности измерений для данного класса или разряда. Углы, лежащие против базисов, должны быть не менее 30°, а прибазисные углы не менее 60°.
Рисунок 13 Схема передачи координат с вершины знака на местность
Исходные данные. Координаты пунктов А, В и С, т.е. ХА, YA, ХВ, YВ, ХС, YС. Измеренные величины: базисы b и b¢; углы b1, b2, b1¢, b2¢, d и d¢. Требуется определить: aАР и ХР, YР. Порядок решения задачи. 1. Из решения обратных геодезических задач по известным координатам пунктов А, В, С находят расстояния SАВ = s, SАС = s¢ и дирекционные углы aАВ и aАС. SAB = SAС = tg aАB = tg aАС = 2. По теореме синусов вычисляют расстояние АР = d дважды из треугольников AMP и ANP d1 = d2 = Разность ½d1 – d2 ½ не должна превышать 2 × 1 / Т, где 1 / Т – предельная относительная погрешность измерения базисов b и b¢. За окончательное значение расстояния принимают d = 3. Вычисление дирекционного угла aАР. Решая треугольники АВР и АРС находят: sin y = sin y¢ = и определяют углы y и y¢. Затем вычисляют углы j и j¢; j = 180° - (d + y) (58) j¢ = 180° - (d ¢+ y¢) (59) По этим углам определяют два значения дирекционного угла aАР. aАР1 = aАВ + j (60) aАР2 = aАС - j¢ (61) Расхождение aАР1 - aАР2 должно удовлетворять неравенству | aАР1 - aАР2 | < 3m, где m – СКП измерения углов. 4. Вычисление координат точки Р, ХР, YР.
ХР2 = ХА + DХАР2; YР2 = YА + DYАР2; (62)
DХАР2 = d cos aАР2 (63) DYАР1 = d sin aАР1 DYАР2 = d sin aАР2 Полученные из двух решений значения координат не должны различаться больше, чем на величину За окончательные значения принимают средние арифметические ХР = YР = aАР = 5. Оценка точности положения точки Р МР = d где mb – CКП измерения базиса b, mb - CКП измерения угла, r¢ = 3438; r¢¢ = 206265 (радианная мера угла).
|


 (50)
(50)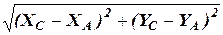 (51)
(51) (52)
(52) (53)
(53) (54)
(54) (55)
(55)
 (56)
(56) (57)
(57) ХР1 = ХА + DХАР1; YР1 = YА + DYАР1;
ХР1 = ХА + DХАР1; YР1 = YА + DYАР1; , где r¢ = 3438.
, где r¢ = 3438.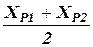 (64)
(64)  (65)
(65) 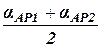 (66)
(66) (67)
(67)


