Прямая засечка (формулы Гаусса)
Если при решении задачи окажется, что видимости между исходными пунктами нет, то применяют формулы Гаусса. Для этого на пунктах А и В измеряют соответственно углы b1 и b2, а для контроля правильности определения координат пункта Р измеряют угол b3 на пункте С (рисунок 17). Исходные данные: ХА, YA; XB, YB; XC, YC. Измеренные углы: b1; b2; b3. Определить: XP и YP. Порядок решения задачи:
a1 = aАР = aАК + b1; a2 = aВР = aBL - b2; a3 = aCР = aCN - b3 Два дирекционных угла необходимы для решения задачи, третий – для контроля и повышения точности. 2. Формулы Гаусса выводятся из известного соотношения tg a1 = откуда: YP – YA = (XP – XA) tg a1 (88) Аналогично получим: YP – YВ = (XP – XВ) tg a2 (89) Эти два равенства представляют систему двух уравнений с двумя неизвестными ХР и YP. Вычтем из уравнения (88) уравнение (89), получим YВ – YA = XP (tg a1 - tg a2) - XA tg a1 + XВ tg a2, откуда XP =
YP = YA + (XP – XA) tg a1 или(91) YP = YВ + (XP – XВ) tg a2 Формулы Гаусса (90) и (91) служат для непосредственного вычисления значений координат пункта Р. 3. Вычтем из обеих частей равенства (90) XA и приведя правую часть к общему знаменателю, будем иметь XP – ХА = Подобно этому найдем XP – ХВ = Полученные два равенства вместе с равенствами (88) и (89) представляют собой формулы Гаусса для приращения координат. Вычислив их, координаты пункта Р определяют дважды:
YP = YА + (YР – YА) = YВ + (YР – YВ)(94) 4. Используя координаты другой пары данных пунктов В и С и соответствующие им дирекционные углы a2 и a3, второй раз вычисляют координаты пункта Р. Например, формулы Гаусса для непосредственных вычислений значений координат пункта Р по второй паре XP = Значение ординаты вычисляют в этом случае по формулам:
YP = YС + (XP – XС) tg a2 5. Оценка точности. Допустимость расхождения между значениями координат, полученными при двух решениях задачи, может быть определена по тем же формулам, что и при решении задачи по формулам Юнга.
|

 1. Вычисляют дирекционные углы a1, a2, и a3
1. Вычисляют дирекционные углы a1, a2, и a3 (87)
(87)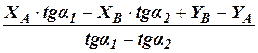 (90)
(90) Значение ординаты вычисляют в этом случае по формулам:
Значение ординаты вычисляют в этом случае по формулам: (92)
(92) (93)
(93) (95)
(95)


