Уравнивание приращений координат
1. Вычисляют координаты узловой точки 2 по трем ходам:
Yi = Yисх + S D уi (126) 2. Вычисляем веса pi = где [S] - длина хода в км 3. Находят среднее весовое (т.е. окончательное значение координат узловой точки)
Yузл = Y0 +
Vx i = Xузл - Хi Vy i = Yузл - Yi (129) Контроль: [ р vx ] = [ p vy] = 0. Полученные поправки распределяют с этим же знаком в ходе пропорционально длинам сторон Vi =
Xi+1 = Xi + D х Yi+1 = Yi + D у (131) 6. Производят оценку точности mх = Мх = где mх – СКП единицы веса; Мх – СКП среднего весового координаты Х. my = Мy = соответственно координаты Y.
Контрольные вопросы
1. Каким образом выполняется построение съемочных ходов? 2. Порядок уравнивания системы нивелирных ходов с одной узловой точкой. 3. Формула для определения окончательного значения высоты узловой точки. 4. В какой последовательности выполняется уравнивание системы теодолитных ходов с одной узловой точкой? 5. По какой формуле определяется окончательное значение дирекционного угла узловой линии? 6. Порядок уравнивания приращений координат. ПРОЕКЦИЯ И ПЛОСКИЕ ПРЯМОУГОЛЬНЫЕ
|
Xi = Xисх + S D хi
, (127)
Хузл = Х0 + 
; где ei = Хi - Х0
(130)
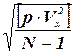(132)
(133)
(134)
(135)
