УРАВНИВАНИЕ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ СГУЩЕНИЯ, ПОСТРОЕННЫХ МЕТОДОМ ТРИАНГУЛЯЦИИ
9.1 Цель и содержание предварительных вычислений в триангуляции 9.2 Цель и содержание уравнительных вычислений в триангуляции 9.3 Виды условных уравнений. Цель и содержание предварительных вычислений в триангуляции
Вычисления в триангуляции являются заключительной частью работ по построению геодезической сети. Вычисления подразделяются на предварительные и уравнительные (окончательные). Целью предварительных вычислений в триангуляции является: 1 определение качества полевых измерений; 2 соответствие их требованиям действующих инструкций; 3 подготовка результатов измерений для дальнейшей обработки, а именно уравнивания и получения координат пунктов, длин сторон и дирекционных углов. Содержание и последовательность предварительных вычислений следующая: 1 Проверка журналов полевых измерений и их оформление; 2 Проверка центрировочных листов и их оформление; 3 Вывод средних значений направлений на каждом пункте и оценка точности угловых измерений, которая производится по формуле:
где m - СКП направления, измеренного одним приемом; К – коррелата; V – уклонения направлений из отдельных приемов от среднего значения; n – число направлений. СКП направления, измеренного Р приемами вычисляют по формуле:
4 Составление рабочей схемы. Исходные пункты наносят по координатам, а остальные пункты засечками по измеренным углам транспортиром. На схеме показывают исходную сторону двойной линией, название пунктов, нумеруют углы и треугольники. 5 Приближенное решение треугольников и вычисление длин сторон с точностью до 1 м. Вычисление сторон начинается от исходной стороны триангуляции по теореме синусов (рисунок 27):
с = q sin C a = q sin A (152) 6 Вычисление поправок в измеренные направления за центрировку и редукцию по формулам:
7 Измеренные направления приводят к центрам пунктов. Поправки за центрировку в измеренные на пункте направления берут из вычислений на данном пункте, а поправку за редукцию – из вычислений на наблюдаемых с него пунктах. 8 По направлениям, приведенным к центрам пунктов, вычисляют углы и в каждом треугольнике подсчитывают невязки w = å b - 180°(155) По навязкам в треугольниках подсчитывают СКП измерения углов в данной сети mb по формуле:
где n – число треугольников в сети.
9.2 Цель и содержание уравнительных вычислений в триангуляции
Конечной целью построения триангуляции является определение координат её пунктов, длин сторон и дирекционных углов. Эта задача может быть выполнена при наличии двух измеренных элементов в каждом треугольнике сети и необходимого числа исходных данных, т.е. координат хотя бы одного пункта сети и дирекционного угла и длины стороны на другой пункт или координат двух пунктов. В этом случае координаты получаются бесконтрольно. Для контроля, повышения точности определения элементов сети и оценки точности измеренных величин обычно измеряют больше элементов, чем это необходимо, т.е. производят избыточные измерения. Каждое избыточное измерение вместе с необходимыми образует математическую зависимость – условие. Например, сумма измеренных углов в треугольнике минус 180°есть невязка w. 1 + 2 + 3 - 180° = w (157) Наличие невязок вносит неопределенность в результаты вычислений искомых величин. Поэтому, прежде чем получить окончательные значения координат пунктов, необходимо устранить все возникающие в сети невязки за те или иные условия путем введения поправок V в измеренные углы, при которых соблюдалось бы равенство: V1 + V2 + V3 + w = 0(158) В данном уравнении три неизвестных. Чтобы однозначно его решить, необходимо ввести дополнительное условие. Таким условием является, чтобы сумма квадратов поправок была минимальной, т.е. [V2] = min. Таким образом, чтобы произвести уравнивание, необходимо: - подсчитать вид и число условий, возникающих в данной сети; - за каждое условие вычислить невязки и допустимую их величину; - вычислить поправки под условием [V2] = min; - ввести эти поправки в измеренные углы и получить уравненные углы; - по уравненным углам вычислить дирекционные углы, длины сторон сети и координаты всех пунктов; - произвести оценку точности уравненных величин.
|

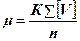 (149)
(149) (150)
(150)
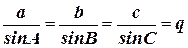 (151)
(151) Приняв сторону b за исходную, находят другие стороны по формулам:
Приняв сторону b за исходную, находят другие стороны по формулам: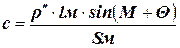 (153)
(153)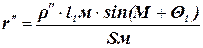 (154)
(154) (156)
(156)


