Редуцирование направлений, линий и площадей на плоскость в проекции Гаусса
Геодезические сети вычисляют в СНГ на плоскостях координатных зон в проекции Гаусса. Но прежде, чем элементы сетей (углы, расстояния) получить на плоскости, их относят (редуцируют) на поверхность референц-эллипсоида. С этой целью измеренные на земной поверхности расстояния приводят к горизонту, затем относят на уровень моря (поверхность квазигеоида) и на поверхность референц-эллипсоида. Переход от расстояний на эллипсоиде к расстояниям на плоскости в проекции Гаусса-Крюгера связан с понятием масштаба изображения. Отношение бесконечно малого отрезка линии на плоскости в проекции Гаусса к соответствующему бесконечно малому отрезку на поверхности эллипсоида называется масштабом изображения. m = Величина и степень изменяемости масштаба изображения являются мерилом искажений линейных элементов на проекции в отдельных ее частях. В каждой точке проекции масштаб различный и искажения зависят от удаления точки от осевого меридиана зоны. Масштаб вдоль осевого меридиана равен единице. Наибольшее искажение получают длины отрезков, находящиеся на краю шестиградусной зоны на широте экватора. Опуская вывод формулы, можем записать, что m = 1 + где Rm – средний радиус кривизны Земли; Rm = 6 371 км. Ym = В проекции Гаусса: - бесконечно малые фигуры подобны соответствующим фигурам на земной поверхности; - не искажаются длины дуг осевых меридианов; - длины других линий и площади фигур получаются искаженными.
|
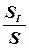(138)
(139)
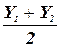- средняя ордината линии.
