Условие полюса
Условие полюса возникает в сетях, имеющих замкнутую цепь треугольников, т.е. где имеется ряд смежных треугольников с общей вершиной, основания которых образуют замкнутую фигуру. Общая вершина называется полюсом. Геометрическое условие полюса выражает требование, чтобы в замкнутой сети треугольников длина любой стороны, вычисленная от произвольно выбранной, но одной и той же стороны по уравненным углам различными путями имела одинаковое численное значение. Например, (рисунок 28), решая треугольники по теореме синусов, получим: S3 = SАВ × S3 =SАВ × Тогда SАВ ×
Решая пропорцию, получим:
Это же условие можно записать в логарифмическом виде (lg sin 2 + lg sin 4 + lg sin 7) – (lg sin 3 + lg sin 6 + lg sin 9) = 0 (176) Данное условие должно соблюдаться по уравненным значениям углов. По измеренным углам данное выражение примет вид: [(lg sin 2 + lg sin 4 + lg sin 7) – (lg sin 3 + lg sin 6 + lg sin 9)] 106 = wП (177) Условное уравнение поправок за условные полюса примет вид: b2 V2 + b4 V4 + b7 V7 - b3 V3 - b6 V6 - b9 V9 + wП = 0 (178) где b2, b4- это изменения логарифмов синусов углов, соответствующие изменениям самих значений углов на одну секунду в шестом знаке логарифма. Знаки коэффициентов b берутся положительными, если угол меньше 90° и отрицательными при углах более 90°. wП доп. = 2,5 mb Число условий полюса вычисляем по формуле: с = р – 2n + 3 (180) где р – число всех сторон в сети (исходных и определяемых); n – число всех пунктов в сети (исходных и определяемых).
|

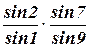 через треугольники АОВ и АОС (172)
через треугольники АОВ и АОС (172)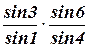 через треугольники АОВ и ОВС (173)
через треугольники АОВ и ОВС (173)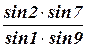 = SАВ ×
= SАВ × 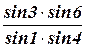 (174)
(174)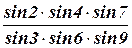 = 1 (175)
= 1 (175) (179)
(179)


