Обратная засечка (формулы Кнейссля)
Привязку ходов можно осуществить, решив задачу по нахождению координат пункта Р по трем исходным А, В, С (рисунок 18), расположенным на значительном расстоянии от определяемого.
Исходные данные: ХА, YA; XB, YB; XC, YC, XD, YD. Измеренные углы: g1; g2; g3. Необходимо определить: XP и YP. Порядок решения задачи: Введем обозначения: aАР = a1; aВР = a2; aCР = a3; ctgg1 = a; ctgg2 = b. Из рисунка 18 видно, что a2 = a1 + g1 Поэтому можно написать: tg a2 = tg (a1 + g1) = 2. Для сокращения записей при дальнейшем выводе перенесем начало координат в точку А. Тогда в новой системе координат будет: Х¢А = 0; Y¢A = 0; X¢B = ХВ - ХА; Y¢B = YB – YA; XC = XC - XA; Y¢C = YC – YA. 3. Известно, что tg aВР = а tg g1 =
Так как Х¢А = 0 и Y¢A = 0, то получим
или (Y¢B - Y¢P)×(a×X¢P + Y¢P) = (X¢B - X¢P)×(a×Y¢P + X¢P) Раскрыв скобки и заново сгруппировав члены, будем иметь
(b×Y¢C - X¢C)× X¢P - (b×X¢C + Y¢C)× Y¢P = -(Х¢) 2 –(Y¢) 2 (100) Обозначив коэффициенты при Х¢ и Y¢ в первом из двух равенств через К1 и К2, а во втором – через К3 и К4, будем иметь систему двух уравнений с двумя неизвестными.
II К3 × X¢P – К4 × Y¢P = - Х¢ 2 - Y¢ 2 (101) Вычтем из первого уравнения второе, получим (К1 – К3) × X¢P -(К2 – К4) × Y¢P = 0, откуда следует, что 4. Обозначим тогда Подставив это выражение в уравнения I и II, получим Y¢P = 5. Определив Y¢P, находят X¢P, подставив это значение в уравнение X¢P = С × Y¢P 6. ХР = X¢P + ХА; YP = Y¢P + YA. (105) 7. сtg aРД = | g3 выч - g3 изм| £ 3 mb, где mb - СКП измерения углов g1; g2; g3. Графическая оценка точности по формулам Г.Е. Сомова определения положения пункта Р, полученного из решения обратной засечки, производится в следующей последовательности. По известным и полученным координатам наносят пункты А, В, С, D и Р в таком масштабе, чтобы не было направлений меньше 5 - 6 см. Измеряют расстояния от пункта Р до исходных пунктов S1, S2, S3 и S4. Вычисляют градиенты направлений по формуле qi = Для графической оценки точности по формулам Г. Е. Сомова определяют средние квадратические погрешности положения пункта Р, полученного соответственно при первом и втором решениях: M1 = M2 = M = где mb - средняя квадратическая погрешность измерения углов.
Рисунок 19 Графическая оценка точности по Г.Е. Сомову
Контрольные вопросы
1. Необходимые исходные данные для определения координат дополнительного пункта прямой засечкой по формулам Юнга. 2. В какой последовательности решается прямая засечка по формулам Гаусса? 3. Последовательность решения обратной засечки по формулам Кнейссля. 4. Каким образом производят определение графической оценки точности по формулам Г.Е. Сомова? 5. Напишите формулу для определения градиентов направлений.
7 УРАВНИВАНИЕ СЪЁМОЧНЫХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ 7.1 Построение съёмочных ходов. 7.2 Уравнивание системы нивелирных ходов с одной узловой точкой 7.3 Уравнивание системы теодолитных ходов с одной узловой точкой
7.1 Построение съёмочных ходов
Съёмочные геодезические сети строят, опираясь на пункты государственной геодезической сети или сетей микротриангуляции, сетей четырехугольников без диагоналей, проложением теодолитных и мензульных ходов, различного вида засечками. Если съёмочная сеть является самостоятельной, то не менее пятой части её пунктов закрепляют постоянными геодезическими знаками по типу грунтового или стенного полигонометрического репера. Обязательному закреплению в данном случае подлежат пункты, на которые переданы координаты, или дирекционные углы с пунктов геодезической сети высшего класса. На все пункты съёмочной геодезической сети передают высоты геометрическим или тригонометрическим нивелированием. В камеральных вычислениях опорных геодезических сетей большое место занимает уравнивание, т.е. распределение невязок в целях получения лучших результатов и выполнения геометрических условий. При построении съёмочной сети нередко бывают случаи, когда между несколькими исходными пунктами прокладывают ходы таким образом, что все они пересекаются в одной точке, которая в таком случае называется узловой.
|

 Для контроля измерений производят наблюдения на пункт D. Таким образом, для решения задачи с контролем необходимо с определяемого пункта Р видеть четыре исходных пункта и измерить при определяемой точке три угла. Наиболее просто эта задача решается с использованием формул Кнейссля.
Для контроля измерений производят наблюдения на пункт D. Таким образом, для решения задачи с контролем необходимо с определяемого пункта Р видеть четыре исходных пункта и измерить при определяемой точке три угла. Наиболее просто эта задача решается с использованием формул Кнейссля. (97)
(97) (98)
(98) . Тогда имеем
. Тогда имеем (99)
(99) ,
, (a×Y¢В - X¢В)× X¢P - (a×X¢В + Y¢В)× Y¢P = -(Х¢) 2 –(Y¢) 2
(a×Y¢В - X¢В)× X¢P - (a×X¢В + Y¢В)× Y¢P = -(Х¢) 2 –(Y¢) 2
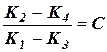 (102)
(102) или X¢P = С × Y¢P(103)
или X¢P = С × Y¢P(103) (104)
(104) ; контроль aРД - aРА = g3 выч (106)
; контроль aРД - aРА = g3 выч (106) ; r²; = 206265. В принятом масштабе градиенты откладывают от пункта Р по соответствующим направлениям, соединяют концы градиентов и получают два инверсионных треугольника DА1В1С1 и DВ1С1Д1 (рисунок 21). Из вершин А1 и С1 первого инверсионного треугольника проводят высоты h1 и h3 на противоположные стороны и измеряют их. Из вершин В1 и Д1 второго инверсионного треугольника аналогично находят h2 и h4.
; r²; = 206265. В принятом масштабе градиенты откладывают от пункта Р по соответствующим направлениям, соединяют концы градиентов и получают два инверсионных треугольника DА1В1С1 и DВ1С1Д1 (рисунок 21). Из вершин А1 и С1 первого инверсионного треугольника проводят высоты h1 и h3 на противоположные стороны и измеряют их. Из вершин В1 и Д1 второго инверсионного треугольника аналогично находят h2 и h4. ; (107)
; (107) ; (108)
; (108) ; (109)
; (109)



