Прямая засечка (формулы Юнга)
В случаях, когда пункты геодезической сети находятся на значительном расстоянии от начала или конца полигонометрического хода, применяют способ привязки прямой засечкой. Задача состоит в нахождении координат пункта по двум исходным пунктам и измеренным при них углам. Для контроля правильности определения координат пункта используют и третий исходный пункт. Угол между смежными направлениями на определяемом пункте должен быть не менее 30° и не более 150°. Существуют различные способы решения задачи. Если между пунктами А и В имеется видимость и измерены при них углы b1 и b2, которые являются углами треугольника АВР (рисунок 16), то для решения задачи применяют формулы Юнга.
ХА, YA; XB, Y B; XC, YC. Измеренные углы: b1; b2; b1¢;; b2¢;. Определить: XP и YP. Порядок решения задачи: Правило: Если с исходной стороны АВ смотреть на определяемый пункт Р, то слева должен быть пункт А, а справа пункт В. Из треугольника АВР по теореме синусов
Соответствующее этой стороне приращение координат определим по известной формуле
Имея в виду формулу (68), а также
можем написать
Из тригонометрии известно, что cos (aАВ - b) = cos aАВ × cos b1 + sin aАВ× sin b1 (72) а sin (b1 + b2) = sin b1× cos b2 + cos b1× sin b2 (73) Подставив данные значения в формулу (71), получим DХАР = Зная, что DХАВ = ХВ – ХА; S × cos aAB = DХАВ = ХВ – ХА; S × sin aAB = DYАВ = YВ – YА, то ХР – ХА = Разделив числитель и знаменатель дроби на произведение sin b1 × sin b2, получим: ХР – ХА = Аналогично найдем YР – YА = Равенства (76) и (77) и есть формулы Юнга для приращений координат. Точно также найдём формулы Юнга для другой пары приращений координат, соответствующие расстоянию ВР = S2 ХР – ХВ = YР – YВ = Вычислив приращения координат по формулам (76) - (79), затем дважды получают координаты пункта Р ХР = ХА + DХАР; YР = YА + DYАР; ХР = ХВ + DХВР; YР = YВ + DYВР; (80) Решив уравнения (76) и (77) относительно ХР и YP и приведя правые части к общему знаменателю, получим формулы Юнга для координат
YР = Контроль вычислений. Вычислив координаты точки Р, можно за исходные взять В и Р, а определяемым - пункт А. Тогда ХА = где g = 180° - (b1 + b2) Для полного контроля правильности определения положения пункта Р, имея координаты пунктов В и С, определяют
YР = Расхождения между координатами, полученными при первом и втором решениях, должны удовлетворять неравенству Ö (х¢ - х²)2 + (у¢ - у²)2 < 3 Мr (84) Мr = Ö М12 + М22 , где М1 и М2 – СКП положения пункта Р, определенного по двум исходным пунктам (А и В; В и С). М1 = М2 = где mb - CКП измерения угла. За окончательные значения координат пункта Р принимают среднее арифметическое из полученных значений при двух решениях М = Мr / 2.
|

 Исходные данные:
Исходные данные: ; (68)
; (68) (69)
(69) (70)
(70) (71)
(71) (74)
(74) (75)
(75)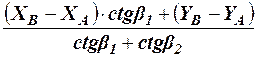 (76)
(76) (77)
(77) (78)
(78) (79)
(79) ХР =
ХР =  (81)
(81)
 (82)
(82) (83)
(83)
 (85)
(85) (86)
(86)


