И сжатии
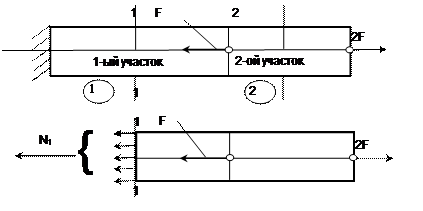
Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила. Брусья с прямолинейной осью (прямые брусья), работающие на растяжение или сжатие, часто называют стержнями. Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют активные силы F и 2F (рис. 2.1). Части бруса постоянного сечения, заключенные между поперечными плоскостями, в которых приложены активные или реактивные силы, будем называть участками. Изображенный на рис. 2.1. брус состоит из двух участков. Применив метод сечений, определим продольные силы
Рис. 2.1.
Для равновесия оставленной части бруса в сечении 1-1 необходимо приложить только силу Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса). Очевидно, что в пределах одного участка продольная сила будет иметь постоянное значение. Следует помнить, что, рассматривая равновесие части бруса, расположенной не справа, а слева от сечения, мы должны были ввести в уравнение равновесия реакцию защемленного конца, определенную путем рассмотрения равновесия всего бруса. В дальнейшем растягивающие (направленные от сечения) продольные силы мы будем считать положительными, а сжимающие (направленные к сечению) - отрицательными. При изучении ряда деформаций мы будем мысленно представлять себе брусья, которые состоят из бесчисленного количества волокон параллельных оси, и предполагать, что при деформации растяжения и сжатия волокна не надавливают друг на друга (это предположение называется гипотезой о ненадавливании волокон). Если изготовить прямой брус из резины (для большей наглядности), нанести на его поверхности сетку продольных и поперечных линий и подвергнуть брус деформации растяжения, то можно отметить следующее: 1) поперечные линии остаются в плоскостях перпендикулярными к оси, а расстояния между ними увеличатся; 2) продольные линии останутся прямыми, а расстояния между ними уменьшатся. Из этого опыта можно сделать вывод, что при растяжении справедлива гипотеза плоских сечений и, следовательно, все волокна бруса удлиняются на одну и ту же величину. Все сказанное выше позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле:
где N - продольная сила; А - площадь поперечного сечения. Очевидно, что при растяжении и сжатии форма сечения на напряжение не влияет. В сечениях, близких к точкам приложения растягивающих или сжимающих сил, закон распределения напряжений по сечению будет более сложным, но мы будем этим пренебрегать и будем считать, что во всех сечениях бруса напряжения распределены равномерно и что в сечении, где к брусу приложена вдоль оси сосредоточенная сила, значения продольной силы и напряжений меняются скачкообразно. Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами, причем для нормальных напряжений применяется то же правило знаков, что и для продольных сил. Перейдем к рассмотрению деформаций. Представим себе прямой брус постоянного поперечного сечения А, длиной
|

 и
и  на участках. Рассечем брус на первом участке поперечным сечением 1-1. Во всех точках бруса будут действовать внутренние распределенные силы, равнодействующая которых определится из условия равновесия одной из частей бруса (например, правой от сечения):
на участках. Рассечем брус на первом участке поперечным сечением 1-1. Во всех точках бруса будут действовать внутренние распределенные силы, равнодействующая которых определится из условия равновесия одной из частей бруса (например, правой от сечения):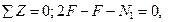 откуда
откуда 
 направленную вдоль оси, т. е. продольную силу. Продольная сила - есть равнодействующая внутренних нормальных сил, возникающих в поперечном сечении бруса. В сечении 2-2 на втором участке продольная сила будет иметь другое значение
направленную вдоль оси, т. е. продольную силу. Продольная сила - есть равнодействующая внутренних нормальных сил, возникающих в поперечном сечении бруса. В сечении 2-2 на втором участке продольная сила будет иметь другое значение 

 жестко защемленный одним концом и нагруженный на другом конце растягивающей силой F. Под действием этой силы брус удлинится на некоторую величину
жестко защемленный одним концом и нагруженный на другом конце растягивающей силой F. Под действием этой силы брус удлинится на некоторую величину  которую назовем абсолютным удлинением. Отношение абсолютного удлинения
которую назовем абсолютным удлинением. Отношение абсолютного удлинения  к первоначальной длине
к первоначальной длине  назовем относительным удлинением и обозначим ε:
назовем относительным удлинением и обозначим ε: 



