Т.е. вторая производная от изгибающего момента по абсциссе сечения балки равна интенсивности распределенной нагрузки.
Построение эпюр изгибающих моментов и поперечных сил Для наглядного представления о характере изменения изгибающего момента и поперечной силы по длине балки и для нахождения опасных сечений строят эпюры M и Q. Технику построения этих эпюр разъясним на следующих примерах. Пример. Построить эпюру М и Q для консольной балки (рис. 5.8 a). Решение. Здесь два участка, (АВ и ВС), различающихся характером нагружения, а следовательно, и законами изменения М и Q.
Рис. 5.8.
Изгибающий момент на участке АВ в сечении, взятом на расстоянии z1 от точки А, найдем как момент левых сил, для чего распределенную нагрузку левее сечения заменяем ее равнодействующей qz1 приложенной в середине участка длиной z1. Получим
Знак минус взят потому, что балка изгибается выпуклостью вверх. Это уравнение параболы. Параболу построим приближенно по трем точкам:
Делаем сечение на участке ВС на расстоянии z2 от свободного конца балки. Распределенную нагрузку на длине а1, заменяем равнодействующей qa1, приложенной в середине участка АВ. Момент в сечении
Это уравнение прямой. Вычисляем МZ при двух значениях z:
Тогда получим
Эпюра М дана на рис. 5.8. Поперечная сила в сечении / — / как сумма проекций на вертикаль левых от сечения сил равна Поперечная сила в сечении //—// равна Q = -qa. Эпюра Q представлена на рис. 5.8 в.
|

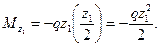 (5.6)
(5.6)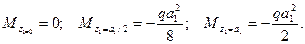 (5.7)
(5.7) (5.8)
(5.8)
 (5.9)
(5.9) .
.


