Объект автоматического управления
Объектом управленияможет быть машина, аппарат, установка, комплекс машин или аппаратов, цех или предприятие. В системах управления часто объектами управления являются системы автоматического регулирования. Состояние объекта или системы характеризуется совокупностью переменных величин - параметров состояния (переменных состояния). Переменные, характеризующие состояние объекта управления, по которым ведется управление, называются управляемыми переменными. Их также называют выходными переменнымиили выходом. Величины, характеризующие внешнее влияние на объект, называются входными воздействиямиили входными сигналами (входом). Воздействия на объект, вырабатываемые управляющим устройством, называют управляющими воздействиями. Внешнее воздействие, определяющее требуемый закон изменения управляемой величины, называется задающим воздействием. Это воздействие поступает от специального задающего устройства (элемента). Воздействия на объект, не зависящие от системы управления, называются возмущающими воздействиями (возмущениями). Различают два вида возмущающих воздействий: · нагрузка; · помехи. Нагрузкойявляется внешнее воздействие, приложенное к управляемому объекту, не зависящее от управляющего устройства и являющееся причиной изменения режима работы объекта. Помехи - это внешние воздействия на отдельные элементы управляющего устройства или объекта управления, не содержащие информации, необходимой для управления. Помехамиявляются ошибки измерительных приборов, сбой в электронных машинах и другие нежелательные явления. Реальные сигналы в системе управления всегда являются смесью полезного сигнала и помехи. На рис. 1.2 схематически показаны переменные, характеризующие воздействия и состояние объекта управления. Здесь: - совокупность управляемых (выходных) переменных обозначена вектором - совокупность управляющих воздействий - вектором - задающих воздействий вектором - - возмущающих воздействий - вектором Совокупность переменных, характеризующая состояние объекта управления, обозначим вектором
Рис. 1.2.
В общем случае вектор у является нелинейной векторной функцией управляющих переменных и внешних воздействий:
Координаты векторов и и у называют соответственно управляющимии управляемыми координатами. Если объект управления характеризуется одной управляющей и одной управляемой величиной, т. е. векторы у и и имеют по одной координате, то объект называется простым, одномерным или односвязным. Если векторы у и и имеют несколько координат, то объект называется многомерным. При наличии нескольких взаимно связанных координат векторов Правило или функциональная зависимость, в соответствии с которой управляющее устройство формирует управляющее воздействие В общем случае эта зависимость может быть записана так:
где F - некоторая, в общем случае нелинейная векторная функция от управляемых переменных у, задающих воздействий g и возмущающих воздействий f. Каждый объект управления может рассматриваться в условиях статики и динамики. В условиях статики компоненты векторов у и и являются постоянными величинами. При изучении динамики объекта исследуется зависимость компонент вектора у от времени, т. е. Параметры объекта могут быть сосредоточенными(постоянными по всем геометрическим координатам) и распределенными(переменными хотя бы по одной координате). Естественно, в первом случае используются обыкновенные дифференциальные уравнения, во втором - дифференциальные уравнения в частных производных (аргументы - время и, по крайней мере, одна геометрическая координата). Для систем, описываемых обыкновенными дифференциальными уравнениями, можно написать
Для решения этой системы уравнений должны быть заданы начальные условия. Если система уравнений (3) может быть сведена к системе линейных дифференциальных уравнений, то объект называется линейным. При описании объекта системой нелинейных дифференциальных уравнений его относят к нелинейным. При изучении статики определяют характер зависимости управляемых координат у от управляющего воздействия и, называемой статической характеристикой объекта. Объект управления может быть устойчивым, неустойчивым и нейтральным. Объект устойчив, если после кратковременного внешнего воздействия он с течением времени возвратится к исходному состоянию или состоянию, близкому к нему.
На рис. 1.3 показаны характеристики устойчивого (рис. 1.3, а), неустойчивого (1.3, б) и нейтрального (1.3, в) объектов. Координата уi в устойчивомобъекте возвращается в исходное состояние после воздействия D u продолжительностью Dt. В неустойчивомобъекте после окончания воздействия отклонение от начальной величины управляемой координаты продолжает увеличиваться. Нейтральнымиобъектами являются такие объекты, в которых по окончании воздействия устанавливается новое состояние равновесия, которое зависит от произведенного воздействия. Механической аналогией здесь является шарик. В лунке (рис. 1.3, а) его положение устойчиво, на вершине холма (рис. 1.2, б) - неустойчиво, а на плоскости (рис. 1.2, в) он в любом месте находится в равновесии.
|

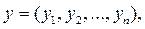


 .
. .Если считать, чтов системе осуществляется управление всеми координатами состояния объекта, то векторы х и у совпадают.
.Если считать, чтов системе осуществляется управление всеми координатами состояния объекта, то векторы х и у совпадают.


 (1)
(1) называется закономили алгоритмом управления.
называется закономили алгоритмом управления. (2)
(2) .
. i =1, 2, …, n. (3)
i =1, 2, …, n. (3) Различают устойчивость “в малом” и устойчивость “в большом”. Некоторые нелинейные объекты могут быть устойчивы “в малом”, т. е. при воздействиях, не превышающих определенные пределы, и неустойчивы “в большом”, т. е. при воздействиях, больших некоторой величины.
Различают устойчивость “в малом” и устойчивость “в большом”. Некоторые нелинейные объекты могут быть устойчивы “в малом”, т. е. при воздействиях, не превышающих определенные пределы, и неустойчивы “в большом”, т. е. при воздействиях, больших некоторой величины.


