Уравнение линии в декартовой системе координат
Любые задатки, прежде чем превратиться в способности, должны пройти большой путь развития. Для многих человеческих способностей это развитие начинается с рождения человека и, если он продолжает заниматься теми видами деятельности, в которых соответствующие способности развиваются, не прекращается до конца жизни. Каждый человек в своем развитии проходит периоды повышенной чувствительности к тем или иным воздействиям, к освоению того или иного вида деятельности. Например, у ребенка в возрасте двух-трех лет интенсивно развивается устная речь, в пять-семь лет он наиболее готов к овладению чтением. В среднем и старшем дошкольном возрасте дети увлеченно играют в ролевые игры и обнаруживают чрезвычайную способность к перевоплощению и вживанию в роли. Важно отметить то, что эти периоды особой готовности к овладению специальными видами деятельности рано или поздно кончаются, и если какая-либо функция не получила своего развития в благоприятный период, то впоследствии ее развитие оказывается чрезвычайно затруднено, а то и вовсе невозможно. Поэтому для развития способностей ребенка важны все этапы его становления как личности. Нельзя думать, что в более старшем возрасте ребенок сможет наверстать упущенное. Развитие способностей в значительной мере зависит от условий, позволяющих реализоваться задаткам. Одним из таких условий являются особенности семейного воспитания. Если родители проявляют заботу о развитии способностей своих детей, то вероятность обнаружения у детей каких-либо способностей более высока, чем когда дети предоставлены сами себе. Другую группу условий развития способностей определяют особенности макросреды. Макросредой принято считать особенности общества, в котором родился и растет человек. Наиболее позитивным фактором макросреды является та ситуация, когда общество проявляет заботу о развитии способностей у своих членов. Для выявления и развития способностей зачастую решающую роль играет труд. Без упорного труда нельзя развить никакую способность, даже если человек обладает самыми блестящими задатками. Д. И. Менделеев писал: «Нет без явно усиленного трудолюбия ни талантов, ни гениев». При этом способности развиваются тем полнее и ярче, чем разнообразнее и содержательнее деятельность человека, чем больший интерес он проявляет к ней. И, наоборот, отношение к работе как к повинности приводит к постепенному угасанию имеющихся способностей. Следовательно, никогда нельзя позволять себе делать что-то «спустя рукава». Методические указания к проведению лекционного занятия Тема № 1.6. Прямые и линии на плоскости План: 1. Уравнение линии на плоскости 2. Различные уравнения прямой 3. Взаимное расположение двух прямых на плоскости 4. Расстояние от точки до прямой
Уравнение линии на плоскости Линия на плоскости рассматривается как множество точек, обладающих некоторыми геометрическими свойствами, только им присущими. Так, окружность радиуса R есть множество всех точек плоскости, удалённых на расстояние R от фиксированной точки О (центра окружности). Введение на плоскости системы координат позволяет определить положение точки плоскости заданием двух чисел – её координат, а положение линии на плоскости определять с помощью уравнения (т.е. равенства, связывающего координаты точек линии). Уравнение линии в декартовой системе координат Уравнением линии (кривой) на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Уравнение линии можно записать в виде F (x, y) = 0, или, если это возможно, в виде y = f (x), где F (x, y), f (x) – некоторые функции. Переменные х и у в уравнении линии называются текущими координатами точек линии. Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения. Для того, чтобы установить лежит ли точка М (x 0, y 0) на заданной кривой, достаточно проверить (не проводя геометрических построений), удовлетворяют ли координаты точки М уравнению этой кривой в выбранной системе координат. Пример. Принадлежат ли точки А (-1; 0) и В (1; 1) линии Решение. Подставим в заданное уравнение вместо х и у координаты точки А, получим 8 · (-1) - 3 · 0 - 5 = - 13 ≠ 0. Следовательно, точка А не лежит на данной линии. Точка В лежит на заданной линии, т.к. 8 · 1 - 3 · 1 - 5 = 0.
Любую кривую можно выразить соответствующим уравнением, хотя на практике это не всегда просто сделать. Но не всякое уравнение определяет на плоскости некую линию. Примеры. Уравнение
Задача нахождения точек пересечения двух линий, заданных уравнениями F 1 (x, y) = 0 и F 2(x, y) = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т.е. сводится к решению системы двух уравнений с двумя неизвестными
Если эта система не имеет действительных решений, то линии не пересекаются.
|

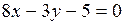 ?
?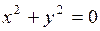 определяет только одну точку (0; 0). Уравнение
определяет только одну точку (0; 0). Уравнение  вообще не определяет ни одной точки на плоскости, т.к. это уравнение не имеет действительных решений.
вообще не определяет ни одной точки на плоскости, т.к. это уравнение не имеет действительных решений.



