Рассмотрим возможные случаи расположения прямых l1 и l2 на плоскости: 1) прямые пересекаются произвольным образом; 2) прямые параллельны; 3) прямые перпендикулярны.

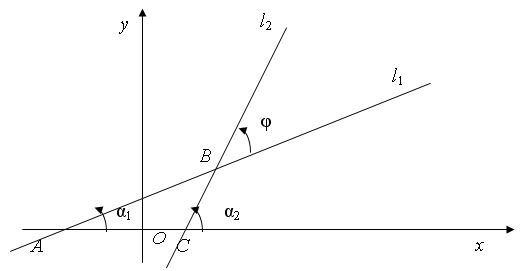
1) Общий случай. Пусть прямые l ₁ и l ₂ пересекаются произвольным образом (рис. 13).

Рис.13. Взаимное расположение двух прямых на плоскости

 

Найдём угол между прямыми. Под углом между прямыми l ₁ и l ₂ понимаем такой угол φ, на который надо повернуть в положительном направлении прямую l ₁ вокруг точки их пересечения В до совпадения с прямой l ₂.

Пусть φ ≠ π/2. Так как α₂ = φ + α₁, (по теореме о внешнем угле треугольника, рассматривая треугольник АВС) или φ = α₂ - α₁, то

.

Но tg α₁ = k ₁, tg α₂ = k ₂, поэтому

. (1)

Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая – второй, то правая часть

 

формулы (1) берётся по модулю, т.е. .

2) Пусть прямые l ₁ и l ₂ параллельны. Тогда φ = 0, tg φ = 0. Из формулы (16) следует k ₂ - k ₁ = 0, т.е. k ₂ = k ₁. И обратно, если прямые l ₁ и l ₂ таковы, что k ₂ = k ₁, то tg φ = 0, т.е. прямые параллельны.

Таким образом, условием параллельности двух прямых l ₁ и l ₂ является равенство их угловых коэффициентов: k ₂ = k ₁.

3) Пусть прямые l ₁ и l ₂ перпендикулярны. Тогда φ = π/2. Следовательно, сtg φ = = 0, откуда 1 + k ₂ k ₁ = 0, т.е. k ₂ k ₁ = - 1. И обратно, если прямые l ₁ и l ₂ таковы, что k ₂ k ₁ = - 1, то сtg φ = 0, т.е. прямые перпендикулярны.

Таким образом, условием перпендикулярности двух прямых l ₁ и l ₂ является равенство: k ₂ k ₁ = - 1.

Если прямые l ₁ и l ₂ заданы на плоскости общими уравнениями А ₁ x + В ₁ у + С ₁ = 0, А ₂ x + В ₂ у + С ₂ = 0, то условия их параллельности и перпендикулярности можно сформулировать следующим образом.

Условием параллельности двух прямых l ₁ и l ₂ является пропорциональность коэффициентов при текущих координатах:

, или, .

Если же ещё и свободные члены пропорциональны, т.е. если

,

то прямые l ₁ и l ₂ совпадают.

Условием перпендикулярности двух прямых l ₁ и l ₂ является равенство:

А ₁ А ₂ + В ₁ В ₂ = 0.