В данном направленииПусть прямая проходит через точку М (х0; у0) и образует с осью Ох угол α ≠ π/2. Так как точка М лежит на прямой, то её координаты удовлетворяют уравнению с угловым коэффициентом (1): у 0 = k x 0 + b. (4) Вычитая равенство (4) из равенства (1), получим уравнение искомой прямой: у - у 0 = k (x - x 0). (5) Уравнение (5) с различными значениями k называют также уравнениями пучка прямых с центром в точке М (х 0; у 0). Из этого пучка нельзя определить лишь прямую, параллельную оси Оу.
Уравнение прямой, проходящей через две точки Пусть прямая проходит через точки М 0 (х 0; у 0) и М 1 (х 1; у 1). Уравнение прямой, проходящей через точку М 0, имеет вид (5): у - у 0 = k (x - x 0), где k - пока неизвестный коэффициент. Так как точка М 1 тоже лежит на прямой, то и её координаты должны удовлетворять уравнению (5): у 1 - у 0 = k (x 1 - x 0). Отсюда найдём
Предполагается, что в уравнении (6) x 1≠ x 0, у 1≠ у 0. Если x 1= x 0, то прямая, проходящая через точки М 0 (х 0; у 0) и М 1 (х 1; у 1), параллельна оси ординат. Её уравнение: x = x 0. Если у 1= у 0, то прямая, проходящая через точки М 0 (х 0; у 0) и М 1 (х 1; у 1), параллельна оси абсцисс. Её уравнение: у = у 0. Пример. Составьте уравнение прямой, проходящей через точки А (2; - 1) и В (- 3; 5). Решение. По уравнению (6):
|
. Подставляя найденное значение k в уравнение (5), получим уравнение прямой, проходящей через две точки М 0 (х 0; у 0) и М 1 (х 1; у 1):
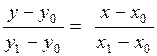. (6)
; 
, откуда после преобразований получим уравнение с угловым коэффициентом: 
, или общее уравнение прямой: 6 x + 5 у - 7= 0.
