Параметрические уравнения линии
Линию на плоскости можно задать при помощи двух уравнений
где х и у - координаты произвольной точки М (х; у), лежащей на данной линии, а t - переменная, называемая параметром. Параметр t определяет положение точки (х; у) на плоскости. Так, если
то значению параметра t = 2 соответствует на плоскости точка (4; 1), т.к. х = 2 + 2 = 4, y = 2 · 2 – 3 = 1. Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания кривой называется параметрическим, а уравнения (1) - параметрическими уравнениями линии. Рассмотрим примерыизвестных кривых, заданных в параметрическом виде. 1) Астроида:
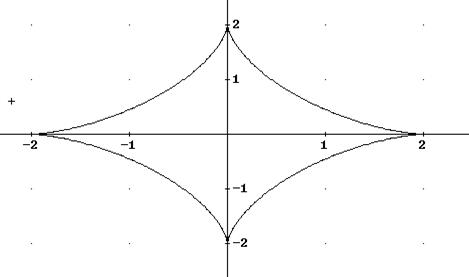
где а > 0 – постоянная величина. При а = 2 имеет вид:
Рис.4. Астроида
2) Циклоида: При а = 2 имеет вид:
Рис.5. Циклоида Векторное уравнение линии
Линию на плоскости можно задать векторным уравнением
где t – скалярный переменный параметр. Каждому значению параметра t 0соответствует определённый вектор Векторному уравнению линии соответствуют два скалярных уравнения (4), т.е. уравнения проекций на оси координат векторного уравнения линии есть её параметрические уравнения.
Рис.6. Векторное уравнение линии
Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, линия – траекторией точки, параметр t - время. Итак, всякой линии на плоскости соответствует некоторое уравнение вида F (x, y) = 0. Отметим ещё раз, что в аналитической геометрии на плоскости решают две основные задачи. Первая: зная геометрические свойства кривой, требуется найти её уравнение. Вторая: зная уравнение кривой, требуется найти её форму и свойства.
|

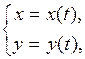 (1)
(1)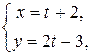
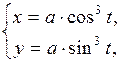
 где а > 0 – постоянная.
где а > 0 – постоянная.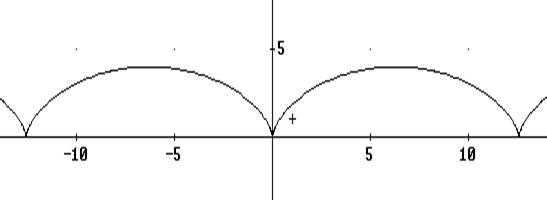
 ,
, плоскости. При изменении параметра t конец вектора
плоскости. При изменении параметра t конец вектора 



