Параметрические уравнения прямойРассмотрим уравнение прямой вида (6). Обозначив равные отношения величиной t, получим
или у - у 0 = t (у 1 - у 0); x - x 0 = t (x 1 - x 0), откуда x = x 0+ t (x 1 - x 0); у = у 0+ t (у 1 - у 0). (7) Уравнения (7) называются параметрическими уравнениями прямой. Заметим, что при t = 0 из уравнений (7) получим координаты точки М 0(х 0; у 0), при t = 1 - координаты точки М 1(х 1; у 1), при 0 < t < 1 - координаты любой внутренней точки отрезка [ М 0 М 1]. Если Уравнение прямой, проходящей через данную точку Перпендикулярно данному вектору Пусть прямая проходит (рис.10) через точку М 0 (х 0; у 0) перпендикулярно ненулевому вектору
Рис.10. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Возьмём на прямой произвольную точку М (х; у) и рассмотрим вектор
или А (х - х 0) + В (у - у 0) = 0. (8) Уравнение (8) называется уравнением прямой, проходящей через данную точку перпендикулярно заданному вектору. Вектор Из уравнения (8), раскрыв скобки, можно получить общее уравнение прямой. Пример. Составьте уравнение прямой, проходящей через точку А (- 3; 1) перпендикулярно вектору Решение. По уравнению (8): -2 (х – (- 3)) + 7(у - 1) = 0. Откуда после преобразований получим общее уравнение прямой: - 2 x + 7 у - 13= 0.
|
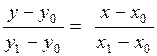= t,
, то точка М (х; у) описывает рассматриваемую прямую.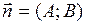
.
= (х - х 0; у - у 0). Поскольку векторы 
и 
= (- 2; 7).
