Не вдаваясь в математические детали, отметим одно важное обстоятельство: любой физически реализуемый периодический процесс может быть представлен в виде суммы гармонических колебаний (быть может в виде бесконечной суммы – интеграла):
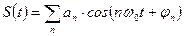
Сумма, которой можно заменить периодический процесс  , называется радом Фурье. Специальный раздел математики – Фурье-анализ - занимается математической стороной проблем, связанных с возможность представления функции
, называется радом Фурье. Специальный раздел математики – Фурье-анализ - занимается математической стороной проблем, связанных с возможность представления функции  в виде ряда. Отметим одно важное свойство такого представления – его единственность. Существует единственный набор необходимых частот
в виде ряда. Отметим одно важное свойство такого представления – его единственность. Существует единственный набор необходимых частот  единственный набор отвечающих этим частотам амплитуд
единственный набор отвечающих этим частотам амплитуд  и начальных фаз
и начальных фаз  , обеспечивающих представление функции
, обеспечивающих представление функции  в виде суперпозиции гармонических функций.
в виде суперпозиции гармонических функций.
Указанное свойство периодической функции (периодического процесса) делает целесообразным во многих физических задачах использовать гармонические колебания.
Рассмотрим пример амплитудно-модулированного колебания  , где амплитуда меняется по закону
, где амплитуда меняется по закону  . Константа
. Константа 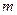 ≤ 1 называется глубиной модуляции.
≤ 1 называется глубиной модуляции.
Для разложения этой функции в ряд Фурье не обязательно пользоваться формулами разложения в ряд, можно использовать простейшие тригонометрические преобразования:
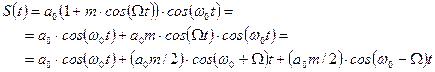
 Итак, амплитудно-модулированное колебание представляется в виде суммы трех гармонических функций (трех гармоник):
Итак, амплитудно-модулированное колебание представляется в виде суммы трех гармонических функций (трех гармоник):
 с частотами
с частотами  ,
,  ,
,  и амплитудами
и амплитудами  ,
, 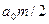 и
и 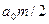 . Колебание
. Колебание  называется несущим колебанием, а
называется несущим колебанием, а  и
и  - боковыми гармониками. Полученный результат удобно изобразить графически, откладывая по оси абсцисс частоты слагаемых гармонических колебаний, по оси ординат – соответствующие этим частотам амплитуды колебаний.
- боковыми гармониками. Полученный результат удобно изобразить графически, откладывая по оси абсцисс частоты слагаемых гармонических колебаний, по оси ординат – соответствующие этим частотам амплитуды колебаний.
Примеры решения задач «Сложение колебаний»

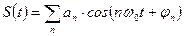
 , называется радом Фурье. Специальный раздел математики – Фурье-анализ - занимается математической стороной проблем, связанных с возможность представления функции
, называется радом Фурье. Специальный раздел математики – Фурье-анализ - занимается математической стороной проблем, связанных с возможность представления функции  единственный набор отвечающих этим частотам амплитуд
единственный набор отвечающих этим частотам амплитуд  и начальных фаз
и начальных фаз  , обеспечивающих представление функции
, обеспечивающих представление функции  , где амплитуда меняется по закону
, где амплитуда меняется по закону  . Константа
. Константа 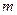 ≤ 1 называется глубиной модуляции.
≤ 1 называется глубиной модуляции.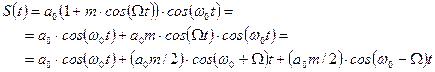
 Итак, амплитудно-модулированное колебание представляется в виде суммы трех гармонических функций (трех гармоник):
Итак, амплитудно-модулированное колебание представляется в виде суммы трех гармонических функций (трех гармоник): с частотами
с частотами  ,
,  ,
,  и амплитудами
и амплитудами  ,
, 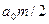 и
и  называется несущим колебанием, а
называется несущим колебанием, а  и
и  - боковыми гармониками. Полученный результат удобно изобразить графически, откладывая по оси абсцисс частоты слагаемых гармонических колебаний, по оси ординат – соответствующие этим частотам амплитуды колебаний.
- боковыми гармониками. Полученный результат удобно изобразить графически, откладывая по оси абсцисс частоты слагаемых гармонических колебаний, по оси ординат – соответствующие этим частотам амплитуды колебаний.


