Вопрос 2. Сложение взаимно перпендикулярных колебаний.Рассмотрим сначала случай, когда материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях, имеющих одну частоту. Проблема заключается в определении траектории точки, которую мы будем в этом случае наблюдать. Пусть одно колебание происходит по оси ОХ, другое – по OY.
Понятно, что точка описывает плоскую траекторию и уравнения
Мы будем видеть колебательное движение точки вдоль прямой, проходящей через начало координат, с амплитудой
Разделив обе части каждого уравнения на А и В соответственно, получаем
Сдвиг по фазе
Если амплитуды колебаний по осям ОХ и OY будут равны А = В, то эллипс преобразуется в окружность радиуса А = В:
Важно заметить, что любое равномерное движение по окружности радиуса А с угловой скоростью Движение по эллипсу тоже может быть разложено на два взаимно перпендикулярных колебания. Более сложной получается траектория точки, совершающей колебания во взаимно перпендикулярных направлениях, если частоты колебаний не равны. В частности, если частоты относятся как целые числа, траектория оказывается замкнутой линией. Такая траектория называются фигурой Лиссажу. Ниже приведены примеры фигур Лиссажу для некоторых значений
|
и 
можно рассматривать как уравнение этой траектории в параметрической форме. Нетрудно видеть, что это - уравнение эллипса, вписанного в прямоугольник со сторонами 
. Ориентация главных осей эллипса зависит от сдвига фаз 
. На рисунке показаны частные случаи таких эллипсов: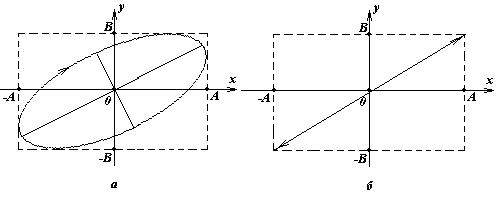
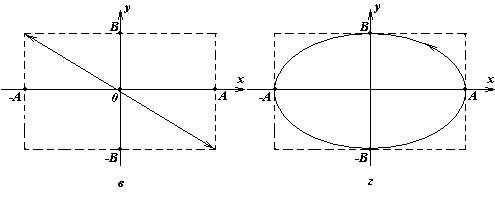
Нетрудно показать, то при сдвиге фаз 
эллипс вырождается в прямую на рисунке б):
.
При 
получаем траекторию на рисунке в):
Траекторией будет эллипс, у которого главные оси совпадают с осями координат так, как показано на рисунке г), если
Покажем это
Возведем каждое уравнение в квадрат и сложим почленно: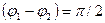
, и против часовой стрелки, если
.
может быть разложено на два взаимно перпендикулярных гармонических колебания с частотой 
и 
