Вопрос 1. Метод векторных диаграмм.
1) Рассчитать среднее значение радиуса шкива r 2) Рассчитать экспериментальные значения момента инерции маховика для грузов массой m1 и m ( 3) Рассчитать средние значения моментов инерции. Занести в таблицы 1, 2. 4) Сравнить численные значения моментов инерции Jzэ и 5) Рассчитать теоретическое значение момента инерции маховика по формуле (20). 6) Сравнить теоретическое значение момента инерции маховика со средними значениями экспериментальных моментов инерции.
Контрольные вопросы.
1. Как определяется момент инерции материальной точки, системы материальных точек, твердого тела? 2. От чего зависит момент инерции твердого тела массой m относительно данной оси вращения z? 3. Каков физический смысл момента инерции твердого тела? 4. Дайте определение момента силы относительно полюса (точки) и неподвижной оси. 5. Каким образом в работе определяется работа сил трения в подшипниках вала? 6. Получите уравнение для расчета момента инерции маховика, пренебрегая трением в подшипниках вала.
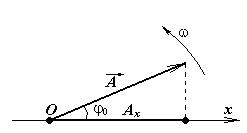
Вопрос 1. Метод векторных диаграмм. 1.1 Вращение вектора. Пусть вектор
  Будем вращать вектор  вокруг точки О с постоянной угловой скоростью w. При этом проекция вектора на ось ОХ будет изменяться. При повороте вектора на угол wt он будет составлять с положительным направлением оси ОХ угол (wt + j0), тогда проекция будет равна
Интересно, что проекция вектора меняется по гармоническому закону, то есть колеблется с циклической частотой w. Этот факт можно использовать для графического представления колебания. Гармоническое колебание величины 1.2 Вращение двух векторов.
Рассмотри два вектора и  с общим началом в точке О. В начальный момент эти вектора составляют с положительным направлением оси ОХ углы jОА и jОВ соответственно.
Будем вращать вектора Построим по правилу параллелограмма сумму векторов
Посмотрим, как ведут себя проекции векторов. Как было показано ранее, проекции вращающихся векторов колеблются с циклической частотой w:
С другой стороны, как видно из рисунка, проекция вектора  равна сумме проекций векторов и :
где jОС - угол, который вектор Нетрудно видеть, что сумма двух гармонических функций одной частоты
|
и внести в таблицы 1, 2.
) по формуле (19). Полученные значения занести в таблицы 1, 2.
, сделать вывод.
Очевидно, что проекция вектора 
изображают вектором 
, длина которого равна амплитуде колебания 
, а угол между вектором и горизонтальной осью ОХ – начальной фазе колебаний 
.
. Нетрудно видеть, что при вращении векторов 
есть гармоническая функция той же частоты 
.
