Рассмотрим обратную задачу.
Пусть требуется найти сумму двух гармонических функций Если А ¹ В, то решить задачу алгебраически непросто (вынести числовой коэффициент за скобки и воспользоваться формулой суммы косинусов нельзя). Это не значит, что алгебраически решить задачу нельзя! Но есть прием, который существенно упрощает работу. Достаточно вспомнить два предыдущих примера. Сумма двух гармонических функций одной частоты есть тоже гармоническая функция той же частоты - см. выражение (1). Ответ можно записать сразу!! Задача сводится к нахождению амплитуды результирующей функции С и ее начальной фазы jОС. Заменим алгебраическую задачу на геометрическую: будем складывать не гармонические функции, а вектора. Для это сделаем следующее: · Построим ось ОХ, отметим на ней точку О. · Построим вектор · Построим вектор · Построим вектор ·
Найдем длину вектора  по теореме косинусов – это будет амплитуда результирующей функции.
·
Найдем угол, который вектор составляет в начальный момент с положительным направлением оси ОХ.
Итак, задача решена.
Где значения С и jОС могут быть найдены по формулам (2) и (3).
Рассмотрим самый простой пример. Найдите сумму
Заметим, что sina = cos(a - p/2). Тогда · Строим вектор · Строим вектор ·
Сумму векторов  по правилу параллелограмма (правило треугольника тоже не возбраняется!)
· Модуль вектора
·
Для угла jОС проще всего найти тангенс Окончательный результат
1.4 Возвращаемся к физике.
Амплитуда результирующего колебания, как мы показали ранее, зависит не только от амплитуд накладываемых колебаний, но и от разности начальных фаз складываемых колебаний. 1. Пусть j01 - j02 = 2pk, где k = 0, 1, 2,… Такие колебания называются синфазными. На векторной диаграмме это выглядит так:
Синфазные колебания усиливают друг друга!
2. Пусть j01 - j02 = (2k -1)p, где k = 0, 1, 2,… В этом случае говорят, что колебания происходят в противофазе. Векторная диаграмма выглядит следующим образом
В этом случае говорят, что колебания ослабляют друг друга. Очевидно, что при А1 = А2 результирующая амплитуда вообще будет равной нулю. Это означает, что тело не будет двигаться вообще. Колебания погасили друг друга. 3. Во всех остальных случаях, когда колебания не будут синфазными или противофазными, мы будем видеть колебания с амплитудой, большей
Полученные результаты имеют бесчисленное множество применений. Забегая вперед, скажем, что если, например, в определенном месте пространства происходят звуковые колебания под действием двух источников, то результирующая громкость звука может оказаться меньше, чем громкость, создаваемая каждым источником в отдельности. Если звуки, создаваемые каждым источником в отдельности, имеют одинаковую интенсивность, то при подходящих условиях эти звуки гасят друг друга, и можно сказать, что «звук + звук = молчание». Возможны также условия, когда два пучка света, падающие на экран, дают не большую, а меньшую освещенность, чем каждый пучок в отдельности; возможен даже случай, когда «свет + свет = темнота». Но об этом позже…
|
с началом в точке О длины А, повернутый относительно оси на угол jОА.
с началом в точке О длины В, повернутый относительно оси на угол jОВ.
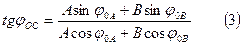
При наложении двух колебаний одной частоты, происходящих вдоль одной прямой мы будем видеть не два движения, а одно. Тело будет совершать колебания вдоль оси ОХ с той же частотой w, изменятся лишь амплитуда и начальная фаза результирующего колебания.
Амплитуда результирующего колебания равна сумме амплитуд слагаемых колебаний
Интересно, что энергия суммарного колебательного движения, пропорциональная квадрату амплитуды, не равна сумме энергий каждого колебания по отдельности, ибо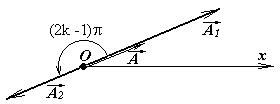
Если А1 > А2, то результирующее колебание происходит синфазно с первым колебанием. Но амплитуда результирующего колебания уменьшилась:
, но меньшей, чем 
.
