Соотношение неопределенностей Гейзенберга.
Отметим, что В рамках концепции корпускулярно-волнового дуализма частиц запишем известное соотношение из теории волн:
 к волновому пакету де-Бройля, до множил на ħ => к волновому пакету де-Бройля, до множил на ħ =>  . Здесь . Здесь  – неопределенность импульса частицы, а – неопределенность импульса частицы, а  – неопределенность координаты. Это соотношение получило название соотношение неопределенностей Гейзенберга и более строго оно записывается так: – неопределенность координаты. Это соотношение получило название соотношение неопределенностей Гейзенберга и более строго оно записывается так: 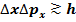 . Гейзенберг интерпретировал данное соотношение следующим образом: если мы измеряем локализацию частицы, то есть, её местоположение, то, в результате, многочисленных измерений, мы получим некоторое среднее значение x0. Результат же конкретного измерения идеальным прибором (прибором без погрешности) будет давать значения (интервал) отсюда . Гейзенберг интерпретировал данное соотношение следующим образом: если мы измеряем локализацию частицы, то есть, её местоположение, то, в результате, многочисленных измерений, мы получим некоторое среднее значение x0. Результат же конкретного измерения идеальным прибором (прибором без погрешности) будет давать значения (интервал) отсюда  и получило название неопределенной координаты. и получило название неопределенной координаты.
Точно так же рассуждения можно провести и для неопределенности импульса Из соотношения неопределенностей следует, что, если мы попытаемся максимально точно измерить местоположение частицы ( Соотношение неопределенности Гейзенберга фактически отражает вероятностный характер поведения микрочастиц. С математической точки зрения соотношение неопределенностей означает, что координата и проекция импульса являются взаимоисключающими переменными и одновременно не могут быть измерены точно (отметим, что речь идет с использованием абсолютно точного прибора). В квантовой механике, кроме приведенных выше, существуют и другие пары взаимоисключающих переменных
ГЛАВА 2: МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ. 9. Волновая функция и её основные свойства. Хорошо известно, что в квантовой механике состояние любой частицы определяется тремя координатами и тремя проекциями импульса, то есть шестью скалярными функциями. Если мы имеем уравнения движения или закон движения (уравнения Ньютона, Лагранжа, Гамильтона) и знаем начальные условия, то есть местоположение частицы в начальный момент времени, то решив уравнения движения, мы будем знать траекторию, а, следовательно, и состояние частицы в любой момент времени, такой подход называется классическим детерминизмом. В квантовой механике состояние частицы принято описывать так называемой волновой функцией: В самом простейшем случае под состоянием микрочастицы мы будем понимать её местоположение в пространстве. В квантовой механике постулируется, что волновая функция подчиняется уравнению Шрёдингера, решив которое, с учётом начального значения волновой функции, мы получим волновую функцию в произвольный момент времени, то есть Рассмотрим основные свойства волновой функции ( Волновая функция в квантовой механике обязана, подчинятся трем основным требованиям: 1. непрерывность; 2. однозначность; 3. конечность. Для волновой функции считается справедливым принцип суперпозиции состояния. Суть его в следующем: если микрочастицы могут находиться в состоянии волновой функции Отметим, что введенная здесь волновая функция зависит от координат времени, но не зависит от импульсов частиц. Это связанно с принципом неопределенности Гейзенберга, из которого следует, что координаты и импульс являются взаимоисключающими переменными. Представление волновой функции в виде:
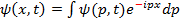 . .
|

 в левой части содержит характеристику частицы импульса p, а в правой – характеристику волны 𝛌. Именно эта формула нагляднее всего свидетельств о корпускулярно-волновом дуализме в отношении частиц и более широком смысле объясняет вероятностные свойства микромира.
в левой части содержит характеристику частицы импульса p, а в правой – характеристику волны 𝛌. Именно эта формула нагляднее всего свидетельств о корпускулярно-волновом дуализме в отношении частиц и более широком смысле объясняет вероятностные свойства микромира. . Это соотношение записано для произвольного волнового пакета и
. Это соотношение записано для произвольного волнового пакета и  - число волновых чисел из которых состоит волновой пакет или, другими словами, область локализации волнового пакета в пространстве волновых чисел.
- число волновых чисел из которых состоит волновой пакет или, другими словами, область локализации волнового пакета в пространстве волновых чисел.


 , то неопределенность импульса проекции будет бесконечно возрастать, и мы ничего не сможем сказать о его численном значении. Наоборот, если мы стремимся максимально точно измерить импульс, то есть,
, то неопределенность импульса проекции будет бесконечно возрастать, и мы ничего не сможем сказать о его численном значении. Наоборот, если мы стремимся максимально точно измерить импульс, то есть,  из соотношения неопределённости следует, что
из соотношения неопределённости следует, что  . Последнее означает, что мы не сможем узнать, в каком месте пространства находится частица.
. Последнее означает, что мы не сможем узнать, в каком месте пространства находится частица.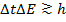 . Здесь
. Здесь  . Кроме этого, нельзя одновременно измерить 2 проекции момента импульса на разные оси координат.
. Кроме этого, нельзя одновременно измерить 2 проекции момента импульса на разные оси координат.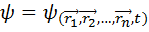 ;
;  . Зная волновую функцию, мы можем определить вероятность состояния микрочастицы следующим образом:
. Зная волновую функцию, мы можем определить вероятность состояния микрочастицы следующим образом:  .
. ;
;  =>
=>  , то есть вероятность состояния микрочастицы в любой произвольный момент времени зависит от вероятности состояния в начальный момент времени, такой подход называется квантовый детерминизм.
, то есть вероятность состояния микрочастицы в любой произвольный момент времени зависит от вероятности состояния в начальный момент времени, такой подход называется квантовый детерминизм. ;
;  ;
;  ;
;  ): 1) нормировка волновой функции
): 1) нормировка волновой функции  .
. , то эти частицы могут находиться в состоянии
, то эти частицы могут находиться в состоянии  .
.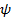 =
=  (x, t) называется x представлением (<x>) или координатным представлением. Однако, в квантовой механике существует возможность использовать и другие переменные в качестве основных
(x, t) называется x представлением (<x>) или координатным представлением. Однако, в квантовой механике существует возможность использовать и другие переменные в качестве основных  (импульсное представление.
(импульсное представление. , <
, <  -энергетическое представление (эпсилон представление).
-энергетическое представление (эпсилон представление). ; dW.
; dW.



