Уравнение на собственное значение. Собственная функция и собственное значение оператора физической величины. Спектр собственного значения.
Отметим, если мы произведем единичные измерения физической величины L, то её дисперсия по определению равна нулю ( Тогда из предыдущего параграфа следует, что
Решение этого оператора уравнения, обязательно удовлетворяющее свойствам конечности, например: однозначность волновой функции 𝛙. …. этим требованиям, как правило, приводим к тому, что решим, возможно, не при любых произвольных значениях физической величины L, а лишь при избранных: В квантовой механике постулируется, что идеальный прибор измерения физической величины L, не может показывать иных значений, кроме собственных значений этой величины.
|
), поскольку 
.
– этот оператор уравнения называется уравнением на собственное значение. В квантовой механике, в подавляющем большинстве случаев, в качестве оператора 
выступает какой-либо дифференциальный оператор первого или второго порядка. Например: 
.
. Такие значения называют собственными значениями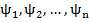 
.
