ПРЯМЫЕ ЗАДАЧИ
1. Рассмотрим, например, как мог сформироваться арифметический способ решения следующей задачи, которую мы отнесли к классу прямых: величина одного поля а, а другого Ь; определить величину поля В, полученного в результате соединения этих полей (или величину поля, полученного при вычитании полей, когда от поля величиной а отрезали поле величиной Ь). На первом этапе, естественно, эта задача должна была решаться с помощью уже сложившихся способов. По ним решение нужно строить так: первое поле присоединить ко второму (или от первого поля отрезать второе) и полученное поле измерить. Этот процесс можно изобразить в следующей схеме: Конец страницы 249 ¯ Начало страницы 250 ¯
где x1 — первое поле; x2 — второе поле; (О1) — число, выражающее величину первого поля; (О2) — число, выражающее величину второго поля. Символом Новый способ вычисления, по которому нужно сложить числа а и Ь или из числа а вычесть о, может возникнуть, если данная задача в некоторых случаях не решается с помощью описанного здесь способа. Такие случаи возникают, когда поле В нельзя измерить и в то же время необходимо вычислить его величину. В новом способе решения этих задач операции с полями (объединение и отделение) переносятся в знаковый план, а число с, фиксирующее величину поля В, получается непосредственно из данных чисел а и Ь. Необходимым условием для такого решения является знание о том, что «число с — результат измерения двух объединенных полей, имеющих величины а и Ь,— равно сумме чисел а и b». Если обозначить это знание символом А, то строение сформировавшейся процедуры решения задачи можно изобразить следующим образом:
Конец страницы 250 ¯ Начало страницы 251 ¯ Здесь знание А обеспечивает переход от процедуры, изображенной в левом блоке схемы (11), к процедуре, изображенной в правом блоке; операция ΔІ — сложение или вычитание чисел (О\) и (О?) (для других типов прямых задач — это деление или умножение). 2. Для трансляции системы операций, изображенной в модели (11), также должны использоваться рисунки с числами. Например, для задач на соединение полей рисунки с числами должны быть такими:
где а, Ь, с — конкретные числа; для задач на разделение полей — такими:
Здесь в первом случае рисунок поля В получается из рисунка первого поля, когда к нему пририсовывается рисунок второго поля, а во втором случае — когда от рисунка первого поля отчеркивается рисунок второго поля. При трансляции сложившегося способа решения данные рисунки с числами начинают выступать в качестве моделей полей x1 х2, х3; это возможно, так как рисунки с числами по отношению к объектам x1 х2, х3 являются знаками-моделями. В результате действия с полями как бы переносятся в плоскость рисунков: действия с полями имитируются в действиях с рисунками (например, действию пририсовывания ставится в соответствие действие объединения полей, действию отчеркивания — действие отделения). Все это позволяет применять знание А уже непосредственно к рисункам полей:
Конец страницы 251 ¯ Начало страницы 252 ¯ где М1—.рисунок первого поля; М2 — второго; М3—.-третьего; Δ': — операции с рисунками (пририсрвывание и отчеркивание); токой линией, обозначена связь сосуществования между рисунками М\Мг и знаками (Ot), (О2) — в эмпирической интерпретации числами а и b (эта связь «обеспечивается» модельной функцией рисунков полей). Непосредственная связь между знанием А и рисунками и числами может быть изображена так:
где стрелкой обозначена связь отнесения знания А к рисункам с числами, угловыми скобками — связи между рисунками и числами (эти связи образуются за счет операций Δ' и Δ1, см. схему (12). Схемы (12) и (13) позволяют построить описание процедуры решения прямой задачи. В условии этой задачи даны одни элементы — рисунки полей М1, М2, М3 и числа (О1), (О2) — и требуется определить другие — число (О3). Это можно изобразить так:
где угловыми штриховыми скобками обозначены связи между рисунками с числами, заданные в условии задачи. Условимся структуру, изображенную на схеме (14), называть обобщенным объектом задачи. Тогда построение решения прямой задачи можно представить как отнесение знания А к обобщенному объекту прямой задачи — см. схемы (13) и (14),— которое дает возможность построить процедуру. Следовательно, главную роль в построении процедуры решения прямой задачи выполняет знание А, которое позволяет установить связи между известными и неизвестными элементами условия задачи, т. е. между элементами, задан- Конец страницы 252 ¯ Начало страницы 253 ¯ ными в условии задачи, и теми элементами, которые необходимо определить. Именно эти связи указывают на те операции и процедуры, которые нужно осуществить для решения задачи.
|

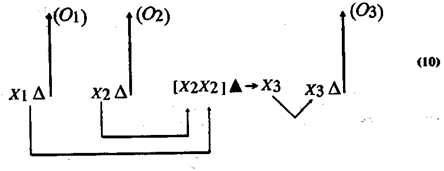
 обозначена операция соединения полей или операция отделения части поля (дальше мы будем говорить просто отделение), В результате операции А. из первого и второго полей получается поле хз, величина которого выражается в числе (О3).
обозначена операция соединения полей или операция отделения части поля (дальше мы будем говорить просто отделение), В результате операции А. из первого и второго полей получается поле хз, величина которого выражается в числе (О3).









