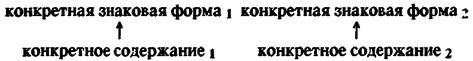IX. СХЕМЫ ДЕЯТЕЛЬНОСТИ УСВОЕНИЯ

В разбираемых нами задачах составление уравнения

­ Конец страницы 406 ­

¯ Начало страницы 407 ¯

обеспечивается совместным применением двух средств. Они составляют то, что может быть названо абстрактным правилом (приемом) составления уравнения для всех задач данного типа. Усвоение этого абстрактного правила предпо-ллагает, с нашей точки зрения, наличие особых процессов. Они конституируют вполне определенный механизм усвоения; специально подчеркнем, что это один- из возможных в ряду многих других механизм.

Как по последовательности, так и в целостном представлении деятельность учащихся по усвоению абстрактного правила (для разбираемого случая и случаев, сходных с ним) может быть представлена следующим образом.

Первый этап — построение прямоугольников по образцу, задаваемому учителем. Обозначим тексты условий задач и совершаемые над этими текстами процедуры, как конкретные содержания, отличия их друг от друга индексами. Получающиеся в итоге этих процедур над текстами изображения прямоугольников назовем конкретными знаковыми формами, имея в виду при введении такого выражения, что в каждом конкретном случае получаемые изображения представляют собой не только итог, но и по функции — форму, накладываемую на конкретные содержания. Употребляемый в обоих случаях эпитет «конкретный» отражает тот простой факт, что учащиеся имеют в данном случае дело с конкретными задачами и не берут их решение как типовое.

Их деятельность может быть представлена (на этом этапе) в виде следующей схемы:

 

 

Кардинален следующий этап. Он начинается с сопоставления конкретных знаковых форм, что на схеме отражено перевернутыми фигурными скобками:

Мы уже показывали, в чем это сопоставление состоит. Выявленные при сопоставлении моменты тождественности должны быть объяснены; объяснение нельзя найти в самих

­ Конец страницы 407 ­

¯ Начало страницы 408 ¯

 

знаковых формах. Отсюда следует необходимость отнесения результатов проделанных сопоставлений к конкретным соде-ржаниям и проведения ряда сопоставлений уже в них:

 

 

Это сопоставление: как показано выше, дает элементы абстрактного правила. Целесообразно назвать совокупность этих элементов абстрактной знаковой формой, подчеркивая тот момент, что она относится не к решению той или иной конкретной задачи, а к типу в целом. Как содержание этой абстрактной знаковой формы выступают уже не условия какой-либо конкретной задачи с процедурами, выполняемыми над ним, а два ряда сопоставлений с отнесением одного ряда сопоставлений к другому. Целесообразно такое содержание обозначить как абстрактное содержание.

Эта схема одного из возможных механизмов усвоения имеет тот смысл, что; во-первых, здесь фиксируется возможный путь овладения абстрактными правилами; во-вторых, подчеркивается, что задание абстрактных правил сразу (на первом этапе) может привести лишь к их заучива-ннию и даже внешне целесообразному употреблению, но не к овладению ими. Если последнее, как показывает школьная практика, иногда имеет место, то такое овладение складывается у учащихся вне целенаправленной дятельности учителя.

­ Конец страницы 408 ­

¯ Начало страницы 409 ¯