ІІ.3. Понятие о нелинейных фракталах

Рассмотренные в п. ІІ.2 фракталы являются линейными потому, что стру-ктуры их инициаторов и генераторов – отрезки прямих линий, которые описы-ваются уравнениями 1-й степени. В бо-льшинстве своём они являются аб-страктными геометрическими конструк-циями, отдалённо или вообще не напо-минающими природные объекты.

Совершенно иначе обстоит дело тогда, когда в качестве элементов ини-циаторов и генераторов выступают кри-вые линии, которые описываются алге-браическими уравнениями различных порядков и потому получаемые фракта-лы называются алгебраическими. Это самая большая группа фракталов. Их получают в результате компьютерного моделирования нелинейных процессов в n-мерных пространствах. Наиболее

изучены процессы и моделирующие их

фракталы, которые описываются квад-ратными уравнениями.

Известно, что нелинейные динами-

ческие системы обладают несколькими

устойчивыми состояниями или аттра-кторами [57].К понятию аттрактора впервые пришел ученый-метеоролог ЭдвардЛоренц, исследуя хаотическое поведение водяного колеса с черпака-ми, на которое льётся вода с большой скоростью. Он выяснил, что в течении длительного времени его вращение мо-жет менять своё направление несколь-ко раз, никогда не достигая постоянной скорости и никогда не повторяясь ка-ким-либо предсказуемым образом.

Моделируя это поведение на ком-пьютере, Лоренц получил на трехмер-ном графике сложную пространствен-ную кривую, витки которой не пересе-каются. Очертания её линий имеют вид крыльев бабочки или двойной спирали в трёхмерном пространстве [40].(рис.ІІ.21).

Непростое, но очень важное поня-тие аттрактора определяет те состоя-ния хаотичного поведения динамичных систем, при которых хаос переходит в порядок.

В связи с большим разнообразием таких систем выявлены разные аттрак-торы, которые классифицированы по числу переменных, необходимых для описания эволюции этих систем во времени. Крупный американский иссле-дователь Билл М. Вильямс по этому поводу писал: «Наука о Хаосе открыла, что всеми внешними явлениями управ-ляют четыре силы, извлекающие поря-док из беспорядка, получившие назва-ние аттракторов: Точечный Аттрактор, Циклический (круговой) Аттрактор, Ат-тракотор Торас и Странный Аттрактор».

[10]. Первый представляется в виде одномерной линии, второй – в виде множества линий в двухмерной плос-кости, третий – в виде множества линий в трёхмерном пространстве, а четвер-тый – в виде множества пульсирующих линий, подобных вибрирующим стру-нам. Четырёхмерность Странного Атт-рактора объясняется наличием вибра-ций. Вильямс утверждает, что когда мы находимся под действием первых трёх аттракторов, нами манипулируют и мы становимся предсказуемыми. Только в

диапазоне Странного Аттрактора мы

можем быть действительно свободны-ми.

Наиболее сложный объект во всей

во всей математике – множество фрак-тальных форм Мандельброта. Его сис-

Рис. ІІ.24. Участок границы фрактала

Мандельброта, увеличенный в 200 раз. (пример эстетики порядка, граничащего с хаосом)

Рис. ІІ.25. Фрактальная картина

Рис. ІІ.26. Увеличенный фрагмент множества Мандельброта

 

 

тема начала проявляться, ко-гда учёный попытался свести к общим законам множества французских математиков Гас-тона Жюлиа и Пьера Фато, (рис. ІІ.22)к описанию которых не подходили понятия евклид-довой геометрии. Обнаружив, что множества Жюлиа явля-ются квадратичными фракта-лами, Мандельброт предло-жил реализовать на компле-ксной плоскости простейший нелинейный алгоритм:

 

Z_n+1 ® Z²_n + C [ 2 ],

 

где знак ® означает итера-цию.

Этот алгоритм позволяет получить числовую последовательность, каждый последующий член которой равен ква-драту предыдущего плюс некоторое слагаемое.

Если в итерационном процессе за-фиксировать значение С и изменять значение Z_n, то получится набор мно-жеств Жюлиа (см. рис. ІІ. 22), а если зафиксировать значение Z_n, то полу-чится множество Мендельброта (рис. ІІ. 23). Это множество структурировано величиной золотой пропорции – 0,618. Оно составлено с помощью винтовых форм и спиралей. Его границы, поража-ющие своей сложностью и своеобра-зной красотой, включают в себя полный набор уменьшенных и деформи-рованных копий множеств Жю-лиа (рис. ІІ. 23 -- ІІ.27).

Исследуя нелинейные зави-симости структуры границ объ-ектов от начальных условий их существования, а также поведе-ние динамичных систем, ученые обнаружили, что вблизи этих границ возникает явление кон-куренции за «обладание» при-граничным пространством. Так происходит переход от хаоса к порядку «снаружи» и «нахожде-ния внутри» и наоборот.

Наблюдая границы своего фрактала, Мандельброт убедил-ся, что при любом увеличении изобра-жения появляются новые формы, похо-жие на морских коньков или на ветви вьющихся растений (рис. ІІ.25). Кроме того, он обнаружил так называемые «плавающие молекулы» или «пылин-ки», которые напоминают островки, ок-ружающие «материк», называемый по –разному: «пряничный человек», «чер-ный карлик», «сердце» (см.рис. ІІ.23).

 

Рис. ІІ.27. Увеличенный фрагментмножества

Мандельброта

 

Американские математики Джон Хаббарт и Андриан Доуди доказали, что каждая плавающая молекула «ви-сит» на филигранной нити, которая связывает её с другими молекулами. В результате образуется хрупкая паутина между этими молекулами и основным объектом. Однако, при дальнейшем увеличении обнаруживались новые мо-лекулы, каждая из которых напоминала систему в целом и одновременно чем-то отличалась от неё. «Это можно назвать чудом миниатюризации: каж-дая новая деталь является вселенной, цельной и многоликой!» [24].

Кстати говоря, простейшая модель итерации последовательностей сумм чисел Фибоначчи 0,1,1,2,3,8,13,… в ка-честве предела последовательных де-лений каждого последующего числа на

предыдущее имеет число 1,618 золото-го сечения.

Оказалось, что именно алгоритмом

 

 

Рис. ІІ.28. Идея концепции динамичного поселения

(от Космоса до Хаоса)

 

Мандельброта пользуется природа, со-здавая свои шедевры – фрактальные

объекты, - от листьев травы до биоло-гических популяций. Поэтому не уди-вительно, что они поразительно краси-вы.

Для очертаний объектов природы – туч, деревьев, снежинок, капель дождя и т.п., характерно определённое чере-дование порядка и беспорядка, космоса и хаоса и представляется, что их гармо-ния является одним из высших принци-пов природы. Под влиянием этой гар-монии формируется наше ощущение прекрасного. Как говорил Гегель: «Мир есть гармония гармоний и дисгармо-ний», а немецкий физик Герт Эйленбер-гер как-то заметил, что наши чувства прекрасно «подпитываются» гармонич-ным сочетанием упорядоченности и беспорядка, устойчивости и хаотично-сти, наблюдаемых в природных явле-ниях.

Геометрической форме присущна масштабность как качественная харак-ристика организуемого ею пространст-ва, заполненного объектами, с которы-ми она вступает в различные метричес-кие соотношения. Исследователи хаоса считают, что произведения истинного искусства не должны иметь единого масштаба в том смысле, что при его создании важные детали должны вы-полняться в разных масштабах. При этом они параллелепипеду небоскреба в Нью-Йорке противопоставляют бароч-ное здание парижской «Гранд Опера», которое по своей природе фрактально, ибо с какого расстояния не рассмотри-вай это строение, всегда найдешь дета-ли, ласкающие взгляд.

Диалектическое единство Хаоса и Космоса присуще всем этапам истории европейского искусства. Так, «рожден-ный из глубин древнегреческой архаики сдержанный и благородный порядок классического искусства Греции сменя-ется вычурным беспорядком искусства эпохи эллинизма. Взятый за образец республиканским Римом порядок клас-сического древнегреческого канона рас-

падается в безудержном хаосе эпохи Римской империи. Затем простота гео-метрического порядка романских хра-мов утопает в каменном кружеве готи-ки, здоровая гармония эпохи Возрож-дения сменяется болезненными изви-вами постренессансного баракко и ро-коко, ритмичный строй классицизма разрушается вихрем романтизма. И уже на нашем веку природный космос критического реализма сменяется ис-кусственным хаосом импрессионизма и модернизма. За внешней пестротой смены различных стилей в европейской истории искусств легко усматривается строгая закономерность взаимных пе-реходов гармонических и дисгармони-ческих стилей, «левополушарных» и «правополушарных» тенденций, апол-лонического и дионисического начал или в общем виде Космоса и Хаоса [11].

В свою очередь, в каждом из выде-ленных периодов обнаруживается пе-риодическая смена гармонических и дисгармонических тенденций. Да и в творчестве отдельного художника при-сутствует «гармония гармонии и дис-гармонии». Примером тому является творчество выдающегося архитектора ХХ века Ле Корбюзье, который боль-шую часть жизни абсолютизирован геометрию и прямой угол, а в послево-енный период, очевидно, стремясь ком-пенсировать нехватку экспрессии и ху-дожественной выразительности своих прежних построек, создал капеллу в Роншане, которая, по словам автора, говорит «языком чистых форм». Под-черкнутый иррационализм этой пост-ройки опрокинул рационалистические каноны, которые сам Корбюзье ранее исповедовал.

Структурный анализ сакральных сооружений различных религий и сим-волики эзотерических школ показывает наличие в них элементов фрактальных конструкций, в фундаментальной гео-метрической основе которых лежит мо-дифицированный крест. Отсюда следу-ет, что не фрактальные формы явля-ются основой фундаменттальных тех-нологий, а наоборот, фундаменталь-ные эзотерические технологии высту-пают проявлением фрактальной струк-туры информационного поля Вселен-ной. Простота фрактальных алгоритмов и великолепие их форм сделали фрак-

тальную геометрию эффективным сре-дством описания морфологических сво-йств природы и человека.

 

ІІ.4. Основные понятия синергетического миропонимания

Слово «синергетика» происходит от греческого «sinergia» - содействие, сотрудничество. Синергизм означает совместное функционирование органов и систем. В широкое употребление тер-мин «синергетика» ввел в 70-е годы ХХ века немецкий физик Г.Хакен., опреде-лив её как науку о саморазвитии или самоорганизации нелинейных систем.

Классическая наука базировалась на лапласовском детерминизме, т.е., на полном исключении неопределённости, на простоте и линейности, что с совре-менной точки зрения несовершенно, так как из рассмотрения исключаются ряд важных факторов, и в первую очередь время и случайность. На этой основе сформировался линейный тип научного мышления, понимавший хаос как деструктивное начало мира, исклю-чавшее из научных теорий случайно-сть как второстепенный фактор, вос-принимавший неравновесность и неус-тойчивость как досадные неприятно-сти, подлежащие преодолению и т.п. При этом развитие понималось как линейное, поступательное, без альтер-натив, и, в силу детерминистской па-радигмы – однозначно предсказуемым.

Вместе с бурным развитием статисти-ческих исследований линейный тип на-учного мышления стал переходить к вероятностному стилю. Квантовая ме-ханика завершила коренной поворот к новой картине мира, в котором вероят-ность, а значит и случайность, приоб-рели статус важных категорий так как было осознано, что случайность и не-определённость коренятся в самой при-роде вещей.

К очередному изменению научного мышления ведёт интенсивное развитие системных исследований и каберне-тики. Новый системный стиль мышле-ния не отвергает вероятностное ви-дение мира, но дополняет его такими важнейшими элементами как сложно-сть, структурность, целенаправленно-сть. Современная наука непосредст-венно «соприкасается с системно-стру-ктурным подходом, с идеями систем-ного анализа, в ходе развития которого

разрабатываются обобщающие идеи,

имеющие значение для современной

теории познания: идеи уровней, иера-рхии, субординации во внутреннем строении и детерминации материаль-ных систем, их автономности относи-тельной независимости, неопределен-ности и случайности в поведении и функционировании» [88].

Синергетику можно рассматривать как современный этап развития идей кибернетики и системных исследова-ний. При этом кибернетика имеет аб-страктно-математический характер, так как абстрагируется от конкретных мате-риальных форм, а синергетика – менее формализованный характер, так как за-нимается исследованием физических основ формирования структур [30].

Основными для кибернетики и об-щей теории систем являются понятия «информации» и «информационного подхода», а в центре внимания синер-гетики – представления о механизмах организации и самоорганизации мате-риальных нелинейных систем. Ведь в нелинейном мире справедливы иные принципы формирования объединения и развития структур, их ускорения и эволюции, которые не могут быть рас-крыты за счет расширения классичес-ких подходов.

Поэтому синергетика, понимающая общую теорию систем как «теорию во-зникновения, существования, преобра-зования и развития систем природы, общества и мышления» [121], обраща-ет особое внимание на понятие разви-тия и связанные с ним понятия само- развития и самоорганизации открытых неравновесных систем, о выборе на-правлений дальнейшей эволюции в так называемых точках бифуркации (точках принятия решений), о существенной и конструктивной роли случайности в этих процессах.

В сравнении с кибернетикой, ко-торая оценивает количество информа-ции, синергетика определяет качество информации или её ценность.

Синергетика изменяет многие при-вычные представления, подвергая ра-дикальной критике стереотипы линей-

ного классического мышления. Она

учит видеть мир по-другому, поражает необычными идеями и представления-

 

 

ми, «поворачивая магический кристалл

знания иной гранью» [ 57].

Еще М.Хайдеггер писал: «Когда ру-шится всё, наступает час философии». Картина мира, которая строилась на протяжении столетий развития класси-ческой и неклассической (квантовой и релятивистской физики) наук, как доэ-волюционная парадигма сейчас суще-ственно меняется. Вновь всплывают и оказываются в фокусе философские, общекультурные и даже мифологичес-кие смыслы чисто внутринаучных про-блем.

Синергетический стиль мышления представляет собой современное сос-тояние постнеклассического системно-го и кибернетического мышления, мно-гие элементы которого подвергаются существенной переделке. Для того, что-бы сформулировать его основные принципы, необходимо погрузить сине-ргетику в среду наследия человеческой культуры, «высветить синергетический кристалл знания под разнонаправлен-ным светом культурных и мировоз-зренческих традиций Востока и Запада, чтобы сделать понятными и доступны-ми основные её идеи и представле-ния» [57].

Несмотря на всю свою новизну, си-нергетика как способ ви¢дения мира и стиль мышления выросла на почве предыдущих стилей научного мышле-ния – детерминистского и вероятност-ного, и несет в себе элементы того и другого. Синергетический стиль мыш--ления представляет собой некоторый синтез позитивных элементов детерми-нистской и вероятностной картин мира. Действительно, динамичность как од-нозначная предопределённость и ста-тичность или, в синергетике, стохасти-чность, случайность, - это характерис-тики двух различных уровней развития и самоорганизации системных объек-тов, т.е., уровня системы как целост-ности и уровня его элементного строе-ния. Динамичность – фундаментальное качество развития системы как целого, ибо оно связано с однонаправленно-стью, однозначной детерминированно-стью развития открытых и неравновес-ных систем между точками бифуркации или точками выбора путей эволюции. А

статичность (стохастичность, случайно-

сть) – такое же фундаментальное ка-чество системы, но относящееся к уро-вню её элементного строения.

В точках бифуркации в состоянии неустойчивости системы возникающие флуктуации, т.е., мгновенные отклоне-ния величин от их средних значений, приобретают макроскопические величи-ны. Тогда хаотические процессы на ми-кроуровне, на уровне элементов систе-мы как бы «пробиваются» на её макро-уровень и приобретают значимость для всей системы в целом.

Флуктуации вносят в картину разви-тия системы определённый элемент неопределённости, определяя выбор одного направления эволюции из це-лого спектра возможных направлений.

В свою очередь, крупнейшие уче-ные современности И.Пригожин, Б.Ман-дельброт, С.Смейл и Г.Хакен обнару-жили, что на границе между конфли-ктами противоположных сил стоит не рождение хаотических структур, как считалось ранее, а происходит спон-танное возникновение самоорганиза-ции порядка более высокого уровня. Более того, структура этой самоорга-низации не статична, а постоянно из-меняется.

Синергетика позволяет снять некие психологические барьеры, страх перед сложными системами благодаря тому пониманию, что сложные социоприро-дные системы являются открытыми и нелинейными и могут описываться не-большим числом фундаментальных идей и образов, а также математиче-ских уравнений, определяющих общие тенденции развёртывания процессов в них.

Синергетика показывает, что от-крытые и нелинейные системы способ-ны к самоорганизации. Их открытость означает наличие в них источников обмена веществом и энергией с окру-жающей средой. Их нелинейность, описываемая математически системой нелинейных уравнений, приобретает физический смысл соответствия множеству их решений множества путей эволюции исследуемой системы.

Основная движущая идея Людвига

фон Берталанфи, основателя общей теории систем, состояла в том, чтобы

 

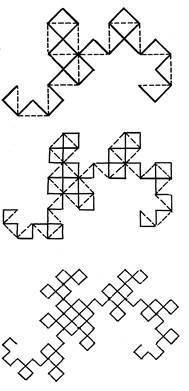
Рис. ІІ.29. Первые три итерации «дракона» Картера-Хейтуэя при неизменяемом инициаторе

Рис. ІІ.30. Последующие три итерации «дракона» Картера-Хейтуэя при неизменяемом инициаторе

 

сделать достояния разных научных ди-

сциплин доступными и сравнимыми

взаимно обогащающими друг друга. Со-временная наука в лице синергетики идёт именно этим путём.