ІІ.5.2. Основы процесса фракталь-ного расширения квадрата

Возможность получения фракталь-ных структур, состоящих из конгруэнт-ных элементов определила желание найти геометрические фигуры такой формы, которые, играя роль комбина-торных, вступающих в замковые соеди-нения, плотно покрывали бы плоскость.

В качестве исходного элемента, ко-торый играет роль и инициатора и гене-ратора, был принят квадрат как наибо-лее технологичная фигура [113,114].

Суть итераций заключается в «расши-рении» квадрата путем прибавления к его сторонам конгруэнтных ему квадра-тов и расширения последующих резу-льтатов итераций за счет прибавления к ним результатов предыдущих итера-ций (рис. ІІ.33 - ІІ.35).

В результате первой итерации ис-ходный квадрат расширился, растя-нулся в двух взаємно-перпендикуляр-ных направлениях или топологически преобразовался в пятиклеточный крест.

В результате второй итерации цен-тральный квадрат пятиклеточного кре-ста расширился или подобно преобра-зовался в девятиклеточный квадрат, а четыре его конца расширились до 5-клеточных крестов. В итоге получилась

29-клеточная фигура, вписанная в 81-клеточный квадрат и имеющая 4 оси симметрии (рис. ІІ.33).

Следует отметить, что в структуру полученной композиции входят 4 золо-тых треугольника, основаниями кото-рых служат стороны квадрата, вписан-ного в исходный квадрат, и 4 двойных квадрата как 16 треугольников Дюрера.

В результате третьей итерации 29-клеточная фигура топологически пре-образуется в 169-клеточную фигуру. (рис.ІІ.34). При этом центральный 9-кле-точный квадрат превращается в 69-клеточную фигуру как 49-клеточный квадрат, к сторонам которого по углам приставлено по одной клетке, а по се-рединам – по три, и 5-клеточные кре-сты – в 29-клеточные, по 4 клетки у ко-торых «забрала» центральная фигура.

Структурный анализ этой фигуры показывает, что она имеет 4 оси сим-

метрии и 5 структурных элементов, 4 из которых, как результаты второй ите-рации, конгруэнтны и взаимосвязаны с центральной фигурой. Эта связь опре-деляется отношением принадлежности к центральной фигуре по 4 клетки каж-дой из боковых фигур.

Рис. ІІ.36. «Срастание» боковых клеток 5-тиклеточного креста с их содержимым с центральной клеткой

 

Рис. ІІ.37. «Срастание» габаритних квадратов боковых169-клеточных фігур с центральной фигурой

 

 

Рис. ІІ.38. Структурированиефигуры наложения габаритних квадратов

 

 

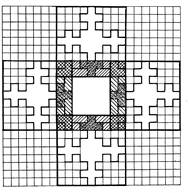
Габаритный квадрат центральной

фигуры является таковым и для резу-

льтата второй итерации. Получается, что габаритные квадраты боковых фи-гур накладываются своими двумя девя-тыми частями на габарит центральной фигуры и в пределах образовавшихся фигур их наложения осуществляется «срастание» центральной фигуры с бо-ковыми (рис. ІІ.36).

В результате 4-й итерации 169-кле-точная фигура топологически расширя-ется до 985-клеточной (рис. ІІ.35). При этом центральная 69-клеточная фигура

расширяется до 405-клеточной, к сто-ронам центрального 121-клето-чного квадрата которой приста-влены 52-клеточные фигуры, а по его углам – 19-клеточные час-ти 29–клеточных результатов второй итерации (рис.ІІ.37). По-лучается, что габаритные квад-раты боковых 169-клеточных фигур своими шестью двадцать третьими частями накладывают-ся на габарит центральной фигу-ры и в пределах образова-вшихся фигур их наложения осуществляется «срастание» це-нтральной части с боковыми.

Конструктивно процесс этого сра-стания происходит путем соответст-вующего структурирования фигур нало-жения габаритных квадратов.

Сущностью процесса срастания бо-ковых фигур с центральной является проникновение в структуру фигуры наложения пограни-чных с нею элементов боко-вых фигур (рис. ІІ.38). В ито-ге фигура наложения струк-турируется результатами второй итерации. Другими словами, в этих фигурах происходят замковые соеди-нения боковых фигур с цен-тральной и процесс их срас-тания можно назвать их «вырастанием» из центра-льной.

Вывод: Процесс фрак-тального расширения квадрата явля-ется геометро-графической моделью динамического процесса роста кле-точных структур живой и неживой природы.

Этот вывод является иллюстра-цией знаменитого афоризма Гераклита

«из одного – всё, из всего – одно» [2] как проявления энергии кундалини, тая-щейся в желуде, из которого выра-стает могучий дуб.