Будем искать частное решение уравнения
в виде
Подставляя предполагаемое решение (25.7) в (25.6), получаем
Сокращая на
Представим знаменатель этого выражения в показательном виде
Модуль этого выражения равен
а аргумент определяется формулой
Подставляя (25.8) и (25.9) в (25.7), найдем:
и, следовательно,
В результате для установившихся вынужденных колебаний напряжения на конденсаторе получаем
где Из (25.11) видно, что амплитуда вынужденных установившихся колебаний
Величина
причем последняя формула верна при Необходимо отметить (проверьте это самостоятельно), что резонансная частота колебаний напряжения на катушке
Уравнение (25.12) определяет форму амплитудно-частотной характеристики (АЧХ) колебаний на конденсаторе, которую называют резонансной кривой (рис. 25.2). Ширина и высота этой кривой зависят от коэффициента Итак, добротность это
Последнее выражение верно при d << w0. Приведем другие выражения для добротности [1, 2]
где l – логарифмический декремент колебаний; R к – активное сопротивление контура. Из (25.12) – (25.14) можно получить при wрез» w0
Ширина резонансной кривой зависит, как отмечалось, от добротности контура. При Q >> 1 резонансный максимум оказывается узким, так что в области резонанса
В этом случае формула (25.16) принимает более простой вид
Рис. 25.2
Обычно ширина резонансной кривой 2Dw измеряется на уровне
где n0= n С – резонансная частота. Из (25.18) видно, что добротность обратна относительной ширине резонансной кривой.
|

 (25.6)
(25.6) . (25.7)
. (25.7) .
. и выражая
и выражая  найдем
найдем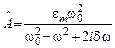 .
. .
. (25.8)
(25.8) . (25.9)
. (25.9)
 . (25.10)
. (25.10) , (25.11)
, (25.11) дает сдвиг фаз между колебаниями напряжения на конденсаторе и колебаниям ЭДС источника.
дает сдвиг фаз между колебаниями напряжения на конденсаторе и колебаниям ЭДС источника. равна
равна . (25.12)
. (25.12) при
при  (резонансная частота) достигает максимума, который равен
(резонансная частота) достигает максимума, который равен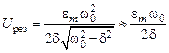 , (25.13)
, (25.13)
 больше, чем
больше, чем  , и, следовательно, резонанс напряжения на LC цепочке наблюдается при промежуточной частоте
, и, следовательно, резонанс напряжения на LC цепочке наблюдается при промежуточной частоте .
. Эта величина называется добротностью колебательного контура
Эта величина называется добротностью колебательного контура  . Физический смысл этого параметра поясняется в лабораторной работе № 23.
. Физический смысл этого параметра поясняется в лабораторной работе № 23. . (25.14)
. (25.14)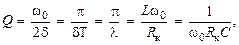 (25.15)
(25.15) . (25.16)
. (25.16) .
. . (25.17)
. (25.17)
 , что соответствует уменьшению мощности колебаний по сравнению с мощностью при резонансе в 2 раза. Подставляя в (25.17)
, что соответствует уменьшению мощности колебаний по сравнению с мощностью при резонансе в 2 раза. Подставляя в (25.17) 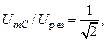 найдем, что ширина резонансной кривой 2Dw на этом уровне и добротность Q связаны соотношением
найдем, что ширина резонансной кривой 2Dw на этом уровне и добротность Q связаны соотношением (25.18)
(25.18)


