Из формул (25.13) и (25.14) следует, что
Следовательно, добротность равна отношению резонансного напряжения U рез на конденсаторе к амплитуде напряжения источника ЭДС e m
т.е. характеризует не только ширину, но и высоту резонансного пика. Вернемся к рассмотрению цепи, изображенной на рис. 25.1. Пусть ЭДС источника изменяется по закону
Воспользовавшись вторым правилом Кирхгофа (25.2) и считая искомой величиной силу тока, получим
Используя комплексное представление правой части (см. (25.6), (25.7)) и считая искомую величину комплексным числом, вместо (25.22) записываем
где Будем искать частное решение уравнения (25.23) в виде
Подставляя (25.24) в (25.23) и сокращая на
Величина, стоящая в квадратных скобках, носит название импеданса контура и обозначается
Выражение для
Это выражение является законом Ома для переменного тока. Роль сопротивления здесь играет Выражение для величины Из формулы (25.26) видно, что импеданс идеального резистора равен R, идеальной катушки i w L, идеального конденсатора Представим импеданс
где
Переходя к действительному выражению для силы тока из (25.24), (25.27) и (25.28), получаем
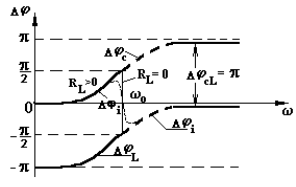
Сравнивая (25.29) и (25.21), видим, что ток отстает по фазе от ЭДС генератора на величину Рассмотрим важные частные случаи: 1. В цепь включено только сопротивление R. Тогда из (25.28) следует, что 2. В цепь включена только емкость С (конденсатор без утечки), из (25.28) 3. В цепь включена только индуктивность L (катушка, активным сопротивлением которой RL можно пренебречь). Из выражения (25.28) следует, что Если теперь рассмотреть цепочку, состоящую из резистора, конденсатора и катушки, в каждом из которых сила тока I за счет последовательного соединения колеблется в одинаковой фазе, то сдвинутыми по фазе относительно друг друга окажутся напряжения на каждом из этих элементов цепи. При этом напряжения на идеальной емкости и идеальной индуктивности всегда окажутся сдвинутыми относительно друг друга по фазе на p радиан (колебания UC и UL – противофазные). Зависимость разности фаз от частоты вынужденных колебаний называется фазочастотной характеристикой (ФЧХ). На рис. 25.3 представлены ФЧХ для емкости Dj С, индуктивности Dj L и LC цепочки Dj L по отношению к колебаниям источника ЭДС. Из формулы (29), кроме того, следует, что при любых значениях активного сопротивления R максимум амплитуды колебаний силы тока достигается при условии
Рис. 25.3
Следовательно, резонансная частота для силы тока равна собственной частоте незатухающих колебаний контура:
|

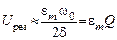 . (25.19)
. (25.19) (25.20)
(25.20) . (25.21)
. (25.21) . (25.22)
. (25.22) , (25.23)
, (25.23) .
.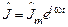 . (25.24)
. (25.24) , получаем
, получаем . (25.25)
. (25.25)
 . (25.26)
. (25.26) . (25.27)
. (25.27)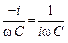 .
. , (25.28)
, (25.28) .
.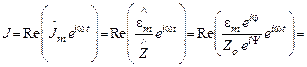
 . (25.29)
. (25.29)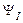 .
. . Колебания тока в активном сопротивлении совпадают по фазе с колебаниями напряжения на нем.
. Колебания тока в активном сопротивлении совпадают по фазе с колебаниями напряжения на нем. . Ток по фазе опережает напряжение на
. Ток по фазе опережает напряжение на  радиан.
радиан. . Ток цепи отстает по фазе от напряжения на
. Ток цепи отстает по фазе от напряжения на  .
.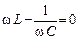 .
.
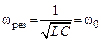 .
.


