Закон полного тока
Закон полного тока(теорема о циркуляции вектора магнитной индукции):циркуляция вдоль замкнутого контура вектора магнитной индукции в вакууме равна произведению магнитной постояннойm0 на алгебраическую сумму токовохватываемых этим контуром:
 , , 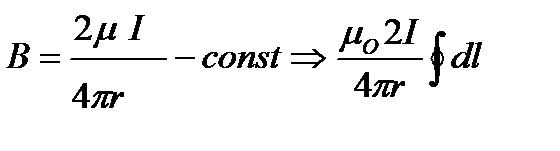
Теорема о циркуляции вектора магнитной индукции есть следствие з-на БСЛ, но она допуск обобщение на поля и люб среды. При таком обобщении эта теорема – одно из обобщ электродинамики Максвелла:
27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида. Применим теорему о циркуляции вектора магнитной индукции. Для вычисления Тороида и длинного соленоида. Тороид – каркас с формой бублика с навитым на него витками проводника по которому течет ток I. Соленоид – цилиндрическая катушка из большого числа намотанного в плотную проводника с током I. Тороид: За контур L возьмем окружность радиуса r так, что контур внутри тороида. Тороид можно рассмотреть как систему последовательно соединенных r круговых токов одинакового радиуса и нанизанных на общую o R круговую ось радиуса R. По теореме циркуляции имеем т.к. контур L проходит внутри тороида, то он охватывает ток равный 2πRnI, где n – число витков на единицу длины – плотность витков. Из симметрии вектор В в каждой точке напр по касй к L, тогда Соленоид: есть тороид бесконечно большого радиуса, т.е R→∞ N Bсол=μ0μnI – магнитное поле соленоида
l
|

 . Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током.
. Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током. . Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.
. Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.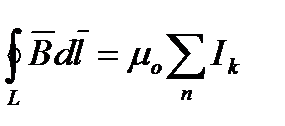
 . Ок-но имеем: В2πr=μ02πRnI =>
. Ок-но имеем: В2πr=μ02πRnI =>  . Если внутри тороида среда с магнитной проницаемостью μ, тогда
. Если внутри тороида среда с магнитной проницаемостью μ, тогда  .
.
 , где N – число витков; l – длина соленоида
, где N – число витков; l – длина соленоида


