Сила Ампера действует на проводник с током, но токи направленное упорядоченное движение зарядов. Тогда сила Ампера должна действовать и на отдельные движущиеся заряды. Найдем исходя из силы Ампера выражение для силы действующей на заряд q движущейся со скоростью 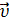 со стороны магнитного поля с индукцией - сила Лоренца.
со стороны магнитного поля с индукцией - сила Лоренца.
B dl Рассмотрим проводник длиной dl и площадью поперечного сечения S в
S магнитном поле с индукцией. Пусть ток в проводнике – I. Заряд q

 со скор
со скор  , а
, а  -концентрация зарядов. На проводник с током q действ сила Ампера:
-концентрация зарядов. На проводник с током q действ сила Ампера:  . Покажем, что эл тока Idl будет э I эквивалентен: qdn
. Покажем, что эл тока Idl будет э I эквивалентен: qdn  , Id
, Id  =qdn
=qdn  , где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d
, где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d  , тогда Id
, тогда Id  =jSd
=jSd  =
=  Sdl => Id
Sdl => Id  =
=  dV, а
dV, а  =qn0
=qn0  dV, где n0dV=dn – число зарядов, тогда Id
dV, где n0dV=dn – число зарядов, тогда Id  =qdn
=qdn  подставим это выражение в формулу для силы Ампера, тогда получим
подставим это выражение в формулу для силы Ампера, тогда получим  – сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:
– сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:  – сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в
– сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в

 К которой лежит
К которой лежит  и В. Направление определяется правилом правого
и В. Направление определяется правилом правого
В и нта. Если вращать рукоятку правого винта от первого вектора υ ко
 α второму вектору В на кратчайший угол α, то поступательное движение
α второму вектору В на кратчайший угол α, то поступательное движение
винта укажет направление силы Лоренца при положительном заряде:  . Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью
. Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью  в эл-ском поле с индукцией, то на заряд будет действовать сила
в эл-ском поле с индукцией, то на заряд будет действовать сила  . Виды траектории зар под действ силы Лоренца: 1. прямая линия
. Виды траектории зар под действ силы Лоренца: 1. прямая линия  ; 2. окружность
; 2. окружность 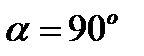 ; 3. цилиндрическая спираль (нарезка винта)
; 3. цилиндрическая спираль (нарезка винта)  .
.
Магнитное взаимод проводника с током и действ магн поля на движ-ся зар предст собой чисто релитивиский эффект. В сист Гаусса выраж для силы:  ,
,  - в сист Гаусса действ магн поля оч мало (много меньш эл-ского).
- в сист Гаусса действ магн поля оч мало (много меньш эл-ского).

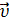 со стороны магнитного поля с индукцией - сила Лоренца.
со стороны магнитного поля с индукцией - сила Лоренца.
 со скор
со скор  , а
, а  . Покажем, что эл тока Idl будет э I эквивалентен: qdn
. Покажем, что эл тока Idl будет э I эквивалентен: qdn  , Id
, Id  =qdn
=qdn  , где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d
, где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d  , тогда Id
, тогда Id  Sdl => Id
Sdl => Id  dV, а
dV, а  – сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:
– сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:  – сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в
– сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в
 К которой лежит
К которой лежит  α второму вектору В на кратчайший угол α, то поступательное движение
α второму вектору В на кратчайший угол α, то поступательное движение . Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью
. Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью  . Виды траектории зар под действ силы Лоренца: 1. прямая линия
. Виды траектории зар под действ силы Лоренца: 1. прямая линия  ; 2. окружность
; 2. окружность 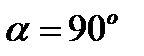 ; 3. цилиндрическая спираль (нарезка винта)
; 3. цилиндрическая спираль (нарезка винта)  .
. ,
,  - в сист Гаусса действ магн поля оч мало (много меньш эл-ского).
- в сист Гаусса действ магн поля оч мало (много меньш эл-ского).


